언덕의 가파른 정도를 기울기라고합니다. 선의 가파름도 마찬가지입니다. 기울기는 두 지점 사이의 수직 변화 인 상승과 동일한 두 지점 사이의 수평 변화 인 런의 비율로 정의됩니다.

$$ slope = \ frac {rise} {run} = \ frac {change \ : in \ : y} {change \ : in \ : x} $$

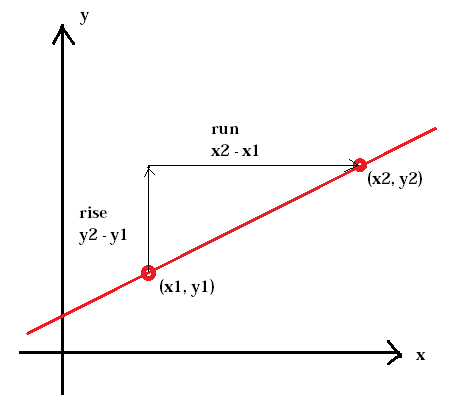
선의 기울기는 일반적으로 문자 m으로 표시됩니다. (x1, y1)은 첫 번째 점을 나타내고 (x2, y2)는 두 번째 점을 나타냅니다.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

분자와 분모 모두에서 x 및 y 좌표를 같은 순서로 유지하는 것이 중요합니다. 그렇지 않으면 잘못된 기울기를 얻게됩니다.

예

선의 기울기 찾기

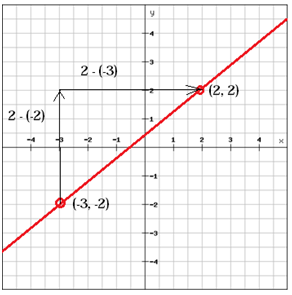
(x1, y1 ) = (-3, -2) 및 (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

양의 기울기 (m > 0)가있는 선은 위의 선과 같이 왼쪽에서 음의 기울기 (m < 0)가있는 선은 왼쪽에서 오른쪽으로 떨어집니다.

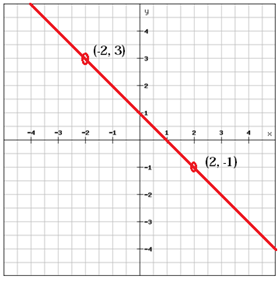
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} =-1 $$

두 선의 기울기가 같으면 선은 p라고합니다. arallel.

기울기 절편 형식을 사용하여 선형 함수를 표현할 수 있습니다.

$$ y = mx + b $$

$$ m = slope $ $

$$ b = y-intercept $$

동영상 강의

경사 찾기