Kraftberechnungen

Kraft ist Drücken oder Ziehen.
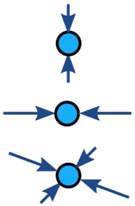
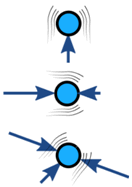
Kräfte auf ein Objekt sind normalerweise ausgeglichen (wenn das Objekt nicht ausgeglichen ist, beschleunigt es):
 |
 |
|
| Ausgeglichen | Unausgeglichen | |
|---|---|---|
| Keine Beschleunigung | Beschleunigung |
Beispiel: Die Kräfte an der Spitze dieses Brückenturms sind ausgeglichen (er beschleunigt nicht):

Die Kabel ziehen sich gleichermaßen nach links und rechts nach unten, und dies wird durch den Aufwärtsschub des Turms ausgeglichen. (Schiebt der Turm? Ja! Stellen Sie sich vor, Sie stehen dort anstelle des Turms.)
Wir können die Kräfte folgendermaßen modellieren:

Und wenn wir Setzen Sie sie von Kopf bis Schwanz, wir sehen, dass sie sich wieder schließen, was bedeutet, dass der Nettoeffekt Null ist:

Die Kräfte sind im Gleichgewicht.
Kräfte im Gleichgewicht sollen sich im Gleichgewicht befinden: Es gibt auch keine Änderung der Bewegung.
Freikörperdiagramme
Der erste Schritt ist Zeichnen eines Freikörperdiagramms (auch als Kraftdiagramm bezeichnet)
Freikörperdiagramm: Eine Skizze, in der ein Körper mit Ausnahme der auf ihn einwirkenden Kräfte von der Welt befreit wird.
Im Brückenbeispiel lautet das Freikörperdiagramm für die Turmspitze:

Freikörperdiagramm
Es hilft Wir sollten klar über die auf den Körper einwirkenden Kräfte nachdenken.
Beispiel: Auto auf einer Autobahn
Welche Kräfte wirken auf ein Auto, das die Autobahn entlang fährt?

Der Motor arbeitet hart. Warum beschleunigt das Auto nicht weiter?
Weil das Fahren Kraft wird ausgeglichen durch:
- Luftwiderstand (einfach ausgedrückt: th Die Luft widersteht dem Herumschieben),
- Rollwiderstand, auch Rollreibung genannt (die Reifen widerstehen einer Formänderung)

Freikörperbild
W ist das Gewicht des Fahrzeugs,
R1 und R2 sind der Rollwiderstand der Reifen,
N1 und N2 sind die Reaktionskräfte (die das Gewicht des Autos ausgleichen).
Hinweis: Stahlräder (wie in Zügen) haben einen geringeren Rollwiderstand, sind aber auf der Straße viel zu rutschig!
Berechnungen
Kraft ist ein Vektor. Ein Vektor hat Größe (Größe) und Richtung:

Wir können die Kräfte modellieren, indem wir Pfeile mit der richtigen Größe und Richtung zeichnen . So:
Beispiel: Bewundern der Ansicht
Brady steht am Rand eines Balkons, der von einem horizontalen Balken und einer Strebe getragen wird:

Er wiegt 80 kg.
Was sind die Kräfte?
Nehmen wir die Stelle ein, auf der er steht, und denken wir über die Kräfte nach:

Sein Gewicht
Seine 80 kg schwere Masse erzeugt aufgrund der Schwerkraft eine nach unten gerichtete Kraft.
Kraft ist Masse mal Beschleunigung: F = ma
Die Beschleunigung aufgrund der Schwerkraft auf der Erde beträgt 9,81 m / s2 , also a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Die anderen Kräfte
Die Kräfte sind ausgeglichen, daher sollten sie sich wie folgt wieder schließen:

Wir können Trigonometrie verwenden, um sie zu lösen
Da es sich um ein rechtwinkliges Dreieck handelt, hilft SOHCAHTOA.
Für den Strahl kennen wir den Nachbarn, wir möchten das Gegenteil kennen, und „TOA“ fordert uns auf, Tangente zu verwenden:
tan (60 ° ) = Strahl / 785 N
Strahl / 785 N = tan (60 °)
Strahl = tan (60 °) × 785 N
Strahl = 1,732 … × 785 N = 1360 N
Für die Strebe kennen wir den Nachbarn, wir möchten die Hypotenuse kennen, und „CAH“ sagt uns, dass wir Cosinus verwenden sollen:
cos (60 °) = 785 N / Strebe
Strebe × cos (60 °) = 785 N
Strebe = 785 N / cos (60 °)
Strebe = 785 N / 0,5 = 1570 N
Gelöst:

Interessant, wie viel Kraft angewendet wird Der Balken und die Strebe im Vergleich zum getragenen Gewicht!
Drehmoment (oder Moment)
Was ist, wenn der Balken nur in der Wand steckt (als Ausleger bezeichnet)?

Es gibt keine Stützstrebe. Was passiert also mit den Kräften?
Das Freikörperdiagramm sieht folgendermaßen aus:

Die Aufwärtskraft R gleicht das Abwärtsgewicht aus.
Nur mit diesen beiden zwingt den Strahl, sich wie ein Propeller zu drehen! Es gibt aber auch einen „Wendeeffekt“ M namens Moment (oder Drehmoment), der dies ausgleicht:
Moment: Kraft mal Abstand im rechten Winkel.
Wir wissen, dass das Gewicht ist 785 N, und wir müssen auch den Abstand im rechten Winkel kennen, der in diesem Fall 3,2 m beträgt.
M = 785 N x 3,2 m = 2512 Nm
Und dieser Moment verhindert, dass sich der Strahl dreht.

Sie können einen Moment spüren, wenn Sie sich an einer Angelrute festhalten.
Sie müssen nicht nur das Gewicht halten, sondern auch verhindern, dass es sich nach unten dreht.
Reibung
Box auf einer Rampe
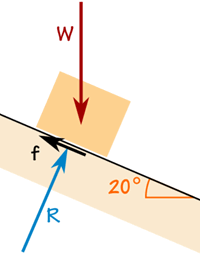
Die Box wiegt 100 kg.
Die Reibungskraft reicht aus, um sie dort zu halten, wo sie ist.
Die Reaktionskraft R steht im rechten Winkel zur Rampe.
Die Box beschleunigt nicht, daher sind die Kräfte im Gleichgewicht:
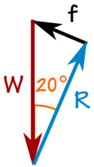
Die 100 kg Masse erzeugt aufgrund der Schwerkraft eine nach unten gerichtete Kraft:
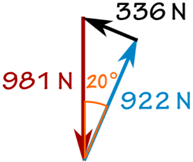
W = 100 kg × 9,81 m / s2 = 981 N
Wir können SOHCAHTOA verwenden, um das Dreieck zu lösen.
Reibung f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reaktion N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Und wir erhalten:
Tipps zum Zeichnen von Freikörperdiagrammen
- Zeichnen Sie so einfach wie möglich. Eine Box ist oft gut genug.
- Kräfte zeigen in die Richtung, in die sie auf den Körper wirken
- gerade Pfeile für Kräfte
- gekrümmte Pfeile für Momente
Sam und Alex ziehen eine Kiste
Die Berechnungen können manchmal einfacher sein, wenn wir Größe und Richtung in x und y umwandeln:
 |
< = > |  |
| Vektor a in polaren Koordinaten |
Vektor a in kartesischen Koordinaten |
Sie können lesen, wie Sie sie in Polar und Kartesisch konvertieren Koordinaten, aber hier ist eine kurze Zusammenfassung:
Verwenden wir sie!