Parametriske og ikke-parametriske tester for å sammenligne to eller flere grupper

Statistikk: Parametriske og ikke-parametriske tester

Denne delen dekker:

• Velge en test
• Parametriske tester
• Ikke-parametriske tester

Velge en test

Når det gjelder valg av en statistisk test, er det viktigste spørsmålet «hva er hovedstudiehypotesen?» I noen tilfeller er det ingen hypotese; etterforskeren vil bare «se hva som er der». For eksempel er det i en prevalensstudie ingen hypotese å teste, og størrelsen på studien bestemmes av hvor nøyaktig etterforskeren vil bestemme prevalensen. Hvis det ikke er noen hypotese, er det ingen statistisk test. Det er viktig å bestemme på forhånd hvilke hypoteser som er bekreftende (det vil si å teste noe forutsatt forhold), og hvilke som er utforskende (er foreslått av dataene). Ingen enkeltstudier kan støtte en hel serie hypoteser. En fornuftig plan er å begrense antallet bekreftende hypoteser sterkt. Selv om det er gyldig å bruke statistiske tester på hypoteser foreslått av dataene, bør P-verdiene bare brukes som retningslinjer, og resultatene behandles som foreløpige til de er bekreftet av påfølgende studier. En nyttig guide er å bruke en Bonferroni-korreksjon, som ganske enkelt sier at hvis man tester n uavhengige hypoteser, bør man bruke et signifikansnivå på 0,05 / n. Dermed hvis det var to uavhengige hypoteser, ville et resultat kun bli erklært signifikant hvis P < 0,025. Merk at siden testene sjelden er uavhengige, er dette en veldig konservativ prosedyre – dvs. en som neppe vil avvise nullhypotesen. Etterforskeren bør da spørre «er dataene uavhengige?» Dette kan være vanskelig å bestemme, men som en tommelfingerregel er resultater på samme person, eller fra matchede individer, ikke uavhengige. Dermed er ikke resultater fra en crossover-prøve, eller fra en case-control-studie der kontrollene ble matchet med tilfellene etter alder, kjønn og sosial klasse, uavhengige.

• Analysen skal gjenspeile designet , og et matchet design bør følges av en matchet analyse.
• Resultater målt over tid krever spesiell forsiktighet. En av de vanligste feilene i statistisk analyse er å behandle korrelerte variabler som om de var
  uavhengige. Anta for eksempel at vi så på behandling av leggsår, der noen mennesker hadde sår på hvert ben. Vi kan ha 20 forsøkspersoner med 30 sår, men antall uavhengige opplysninger er 20 fordi tilstanden til sår på hvert ben for en person kan påvirkes av tilstanden til personens helse og en analyse som betraktet sår som uavhengige observasjoner ville være feil. For en korrekt analyse av blandede og uparede data, kontakt en statistiker.

Det neste spørsmålet er «hvilke typer data blir målt?» Testen som brukes skal bestemmes av dataene. Valget av test for samsvarende eller sammenkoblede data er beskrevet i tabell 1 og for uavhengige data i tabell 2.

Tabell 1 Valg av statistisk test fra sammenkoblet eller matchet observasjon

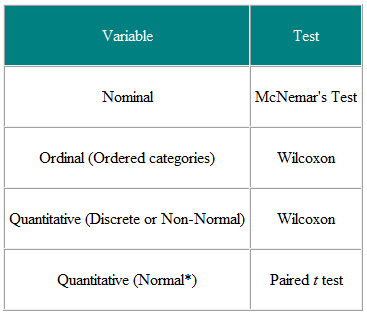
Det er nyttig å bestemme inngangsvariablene og resultatvariablene. For eksempel, i en klinisk studie er inngangsvariabelen typen behandling – en nominell variabel – og resultatet kan være noe klinisk mål, kanskje normalt distribuert. Den nødvendige testen er da t-testen (tabell 2). Imidlertid, hvis inngangsvariabelen er kontinuerlig, si en klinisk score, og utfallet er nominelt, si herdet eller ikke herdet, er logistisk regresjon den nødvendige analysen. En t-test i dette tilfellet kan hjelpe, men vil ikke gi oss det vi trenger, nemlig sannsynligheten for en kur for en gitt verdi av den kliniske poengsummen. Anta at vi har en tverrsnittsstudie der vi spør et tilfeldig utvalg av mennesker om de mener at allmennlegen gjør en god jobb, på en fem-punkts skala, og vi ønsker å fastslå om kvinner har en høyere mening av allmennleger enn menn har. Inngangsvariabelen er kjønn, som er nominell. Utfallsvariabelen er fem-punkts ordinær skala. Hver persons mening er uavhengig av de andre, så vi har uavhengige data. Fra tabell 2 bør vi bruke en χ2-test for trend, eller en Mann-Whitney U-test med en korreksjon for bånd (NB et slips forekommer der to eller flere verdiene er de samme, så det er ingen streng økende rekkefølge på rangene – der dette skjer, kan man gjennomsnittlig rangere for bundne verdier. Vær imidlertid oppmerksom på at hvis noen mennesker deler en allmennlege og andre ikke, så er ikke dataene uavhengig og det kreves en mer sofistikert analyse. Merk at disse tabellene kun skal betraktes som veiledninger, og hvert tilfelle bør vurderes på sin fordel.

Tabell 2 Valg av statistisk test for uavhengige observasjoner

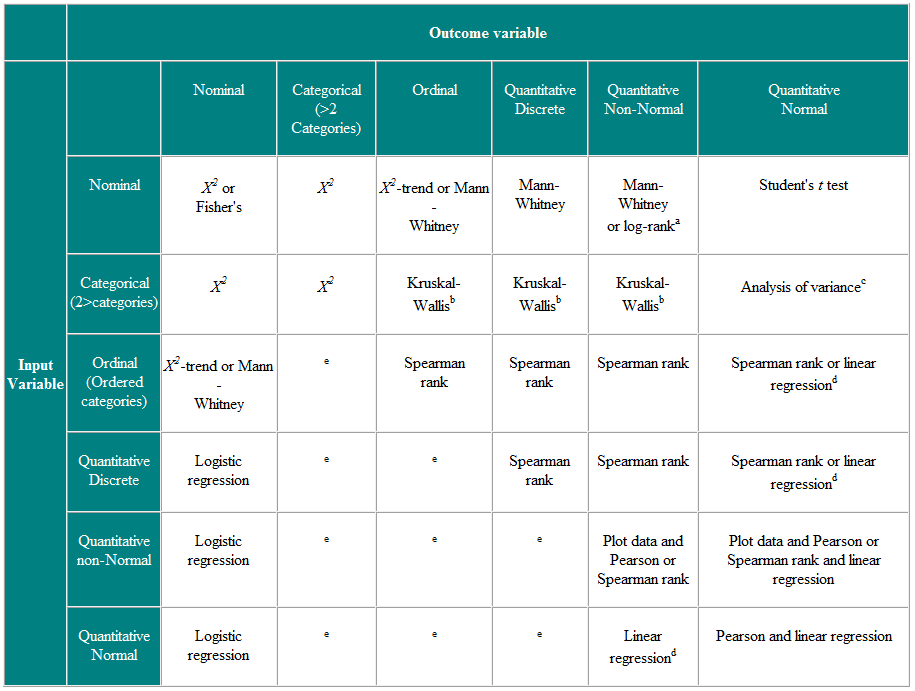
a Hvis data sensureres. b Kruskal-Wallis-testen brukes til å sammenligne ordinale eller ikke-normale variabler for mer enn to grupper, og er en generalisering av Mann-Whitney U-testen. c Variansanalyse er en generell teknikk, og en versjon (enveis variansanalyse) brukes til å sammenligne normalt distribuerte variabler for mer enn to grupper, og er den parametriske ekvivalenten til Kruskal-Wallistest. d Hvis utfallsvariabelen er den avhengige variabelen, så forutsatt at restene (forskjellene mellom de observerte verdiene og de forventede responsene fra regresjon) er sannsynlig Normalt fordelt, så er ikke fordelingen av den uavhengige variabelen viktig. e Det finnes en rekke mer avanserte teknikker, for eksempel Poisson-regresjon, for å håndtere disse situasjonene. Imidlertid krever de visse antakelser, og det er ofte lettere å dikotomisere utfallsvariabelen eller behandle den som kontinuerlig.

Parametriske tester er de som antar parametrene for populasjonsfordelingen som prøven er hentet fra. . Dette er ofte antagelsen om at populasjonsdataene er normalt fordelt. Ikke-parametriske tester er «distribusjonsfrie» og kan som sådan brukes til ikke-normale variabler. Tabell 3 viser den ikke-parametriske ekvivalenten til et antall parametriske tester.

Tabell 3 Parametrisk og Ikke-parametriske tester for å sammenligne to eller flere grupper

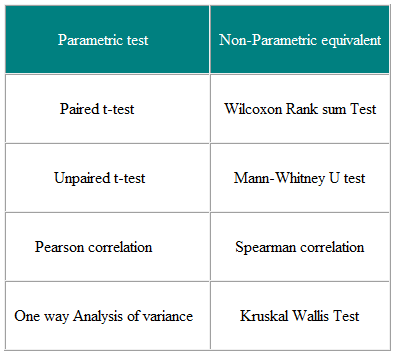
Ikke-parametriske tester er gyldige for både ikke-normalt distribuerte data og Normalt distribuerte data, så hvorfor ikke bruke dem hele tiden?

Det virker fornuftig å bruke ikke-parametriske tester i alle tilfeller, noe som vil spare deg for å teste for normalitet. Parametriske tester foretrekkes, av følgende årsaker:

1. Vi er sjelden interessert i en signifikansetest alene. Vi vil gjerne si noe om populasjonen som prøvene kom fra, og dette gjøres best med
estimater av parametere og konfidensintervaller.

2. Det er vanskelig å gjøre fleksibel modellering med ikke-parametriske tester, for eksempel å tillate forvirrende faktorer ved bruk av flere regresjon.

3. Parametriske tester har vanligvis mer statistisk kraft enn ikke-parametriske ekvivalenter. Med andre ord er det mer sannsynlig at man oppdager signifikante forskjeller når de virkelig eksisterer.

Sammenligner ikke-parametriske tester medianer?

Det er en vanlig tro at en Mann-Whitney U-test er faktisk en test for forskjeller i medianer. Imidlertid kan to grupper ha samme median og likevel ha en signifikant Mann-Whitney U-test. Vurder følgende data for to grupper, hver med 100 observasjoner. Gruppe 1: 98 (0), 1, 2; Gruppe 2: 51 (0), 1, 48 (2). Medianen i begge tilfeller er 0, men fra Mann-Whitney-testen P < 0,0001. Bare hvis vi er forberedt på å anta den ekstra antagelsen om at forskjellen i de to gruppene bare er et skift i plassering (det vil si at fordelingen av dataene i den ene gruppen ganske enkelt forskyves med et fast beløp fra den andre) kan vi si at testen er en test av forskjellen i medianer. Imidlertid, hvis gruppene har samme fordeling, vil et skift i plassering flytte medianer og midler med samme mengde, og så er forskjellen i medianer den samme som forskjellen i gjennomsnitt. Dermed er Mann-Whitney U-testen også en test for forskjellen i middel. Hvordan er Mann-Whitney U-testen relatert til t-testen? Hvis man skulle legge inn rekken av dataene i stedet for selve dataene i et t-testprogram med to eksempler, ville den oppnådde P-verdien være veldig nær den som ble produsert av en Mann-Whitney U-test.