• K-nærmeste nabo er en av de enkleste maskinlæringsalgoritmene basert på Supervised Learning-teknikk.
• K-NN-algoritme antar likheten mellom den nye saken / dataene og tilgjengelige saker og setter den nye saken i den kategorien som er mest lik de tilgjengelige kategoriene.
• K-NN-algoritme lagrer alle tilgjengelige data og klassifiserer et nytt datapunkt basert på likheten. Dette betyr at når nye data vises, kan de lett klassifiseres i en brønnpakke-kategori ved hjelp av K-NN-algoritme.
• K-NN-algoritme kan brukes til regresjon så vel som til klassifisering, men hovedsakelig brukes den til klassifiseringsproblemene.
• K-NN er en ikke-parametrisk algoritme, som betyr den legger ikke til grunn noen underliggende data.
• Det kalles også en lat elevalgoritme fordi den ikke lærer av treningssettet umiddelbart, i stedet lagrer det datasettet og på klassifiseringstidspunktet utfører det et handling på datasettet.
• KNN-algoritme i treningsfasen lagrer bare datasettet, og når det får nye data, klassifiserer det dataene i en kategori som ligner mye på de nye dataene.
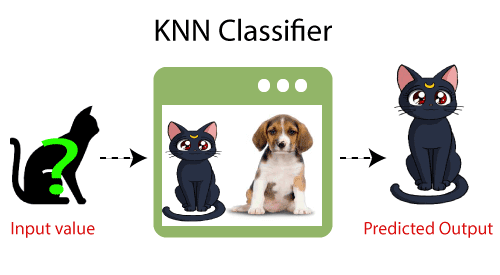
• Eksempel: Anta at vi har et bilde av en skapning som ligner på katt og hund, men vi vil vite om det er en katt eller hund. Så for denne identifikasjonen kan vi bruke KNN-algoritmen, da den fungerer på et likhetsmål. KNN-modellen vår vil finne lignende funksjoner i det nye datasettet til katter og hunder, og basert på de mest lignende funksjonene vil den plassere den i enten katt- eller hundekategori.

Hvorfor trenger vi en K-NN-algoritme?

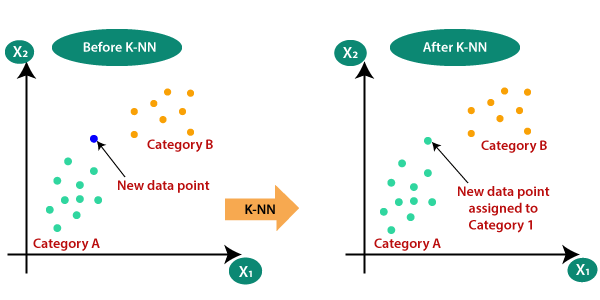
Anta at det er to kategorier, dvs. kategori A og kategori B, og vi har et nytt datapunkt x1, så dette datapunktet vil ligge i hvilken av disse kategoriene. For å løse denne typen problemer trenger vi en K-NN-algoritme. Ved hjelp av K-NN kan vi enkelt identifisere kategorien eller klassen til et bestemt datasett. Tenk på diagrammet nedenfor:

Hvordan fungerer K-NN?

K-NN-arbeidet kan forklares på bakgrunn av algoritmen nedenfor:

• Trinn 1: Velg antall K for naboene
• Trinn 2: Beregn den euklidiske avstanden til K antall naboer
• Trinn 3: Ta de K nærmeste naboene i henhold til den beregnede euklidiske avstanden.
• Trinn 4: Blant disse k naboene, tell antallet datapunkter i hver kategori.
• Trinn 5: Tildel de nye datapunktene til den kategorien som antallet naboer er maksimalt for.
• Trinn 6: Modellen vår er klar.

Anta at vi har et nytt datapunkt, og vi må sette det i ønsket kategori. Tenk på bildet nedenfor:

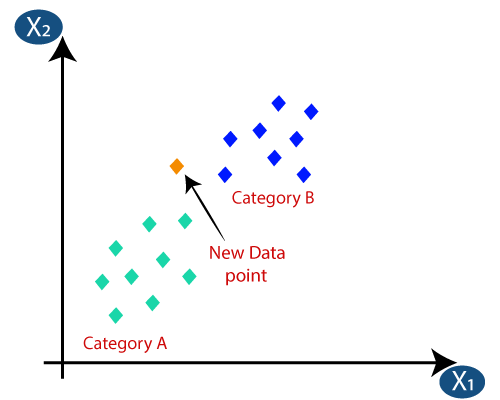
• For det første velger vi antall naboer, så vi velger k = 5.
• Deretter skal vi beregne den euklidiske avstanden mellom datapunktene. Den euklidiske avstanden er avstanden mellom to punkter, som vi allerede har studert i geometri. Det kan beregnes som:

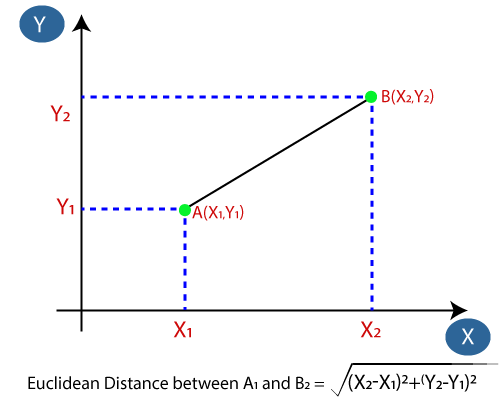
• Ved å beregne den euklidiske avstanden fikk vi de nærmeste naboene, som tre nærmeste naboer i kategori A og to nærmeste naboer i kategori B. Tenk på bildet nedenfor:

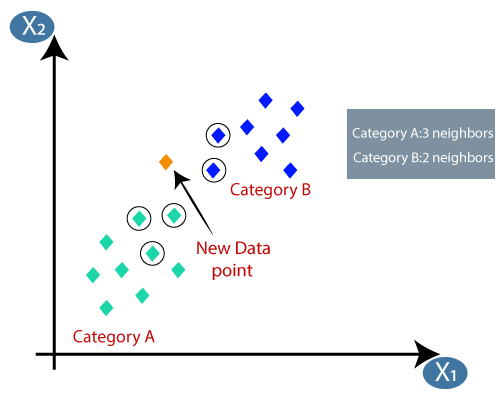
• Som vi kan se er de 3 nærmeste naboene fra kategori A, derfor må dette nye datapunktet tilhøre kategori A.

Hvordan velge verdien av K i K-NN-algoritmen?

Nedenfor er noen punkter til husk mens du valgte verdien av K i K-NN-algoritmen:

• Det er ingen spesiell måte å bestemme den beste verdien for «K», så vi må prøve noen verdier for å finne den beste ut av dem. Den mest foretrukne verdien for K er 5.
• En veldig lav verdi for K som K = 1 eller K = 2, kan være støyende og føre til effekten av outliers i modellen.
• Store verdier for K er gode, men det kan være vanskelige.

Fordeler med KNN-algoritme:

• Det er enkelt å implementere.
• Det er robust mot de støyende treningsdataene
• Det kan være mer effektivt hvis treningsdataene er store.

Ulemper ved KNN-algoritme:

• Må alltid bestemme verdien av K som kan være kompleks en stund.
• Beregningskostnaden er høy på grunn av beregning av avstanden mellom datapunktene for alle treningsprøvene .

Python-implementering av KNN-algoritmen

For å gjøre Python-implementeringen av K-NN-algoritmen, vil vi bruke samme problem og datasett som vi har brukt i Logistisk regresjon. Men her vil vi forbedre ytelsen til modellen. Nedenfor er problembeskrivelsen:

Problem for K-NN algoritme: Det er et bilprodusentfirma som har produsert en ny SUV-bil.Selskapet ønsker å gi annonsene til brukerne som er interessert i å kjøpe SUV-en. Så for dette problemet har vi et datasett som inneholder informasjon om flere brukere gjennom det sosiale nettverket. Datasettet inneholder mye informasjon, men den estimerte lønnen og alderen vi vil vurdere for den uavhengige variabelen, og den kjøpte variabelen er for den avhengige variabelen. Nedenfor er datasettet:

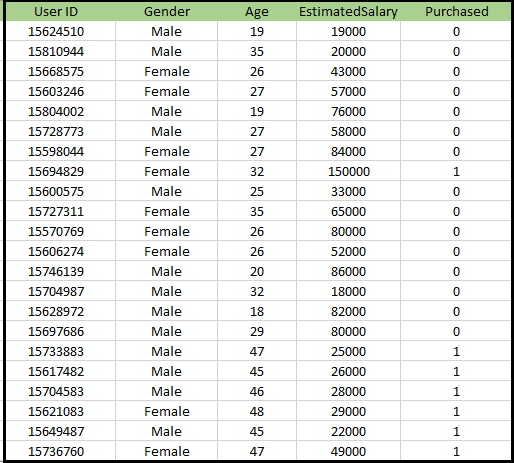
Fremgangsmåte for å implementere K-NN-algoritmen:

• Dataforbehandlingstrinn
• Tilpasse K-NN-algoritmen til treningssettet
• Forutsi testresultatet
• Testnøyaktighet av resultatet (Creation of Confusion matrix)
• Visualisere testsettets resultat.

Databehandlingstrinn:

Databehandlingstrinnet forblir nøyaktig det samme som logistisk regresjon. Nedenfor er koden for det:

Ved å utføre ovennevnte kode, blir datasettet vårt importert til programmet vårt og godt forbehandlet. Etter funksjonsskalering vil testdatasettet vårt se ut:

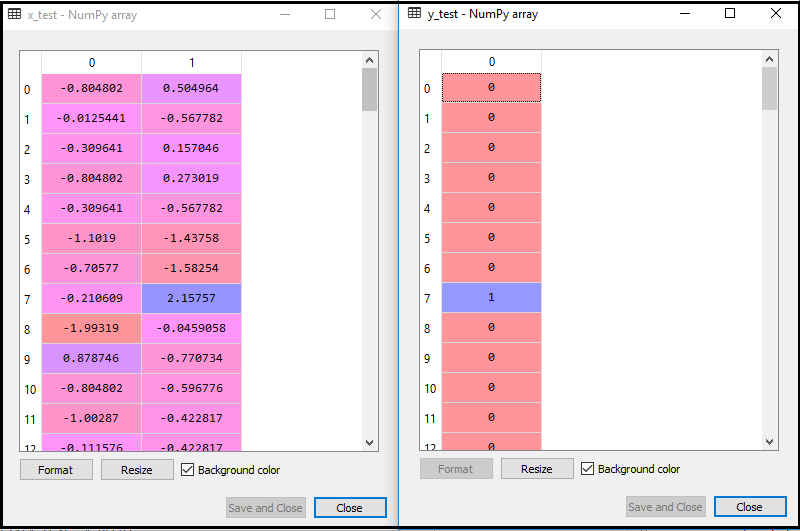
Fra ovennevnte utgang im alder, kan vi se at dataene våre er vellykket skalert.

• Tilpasse K-NN-klassifiseringen til treningsdataene:
  Nå skal vi tilpasse K-NN-klassifisereren til treningsdataene. For å gjøre dette importerer vi KNeighborsClassifier-klassen i Sklearn Neighbors-biblioteket. Etter å ha importert klassen, oppretter vi klassifiseringsobjektet til klassen. Parameteren til denne klassen vil være
  • n_nebors: Å definere de nødvendige naboene til algoritmen. Vanligvis tar det 5.
  • metric = «minkowski»: Dette er standardparameteren og bestemmer avstanden mellom punktene.
  • p = 2: Det tilsvarer standarden Euklidisk beregning.

  Og så passer vi klassifisereren til treningsdataene. Nedenfor er koden for den:

Utgang: Ved å utføre ovennevnte kode, vil vi få utdata som:

• Forutsi testresultatet: For å forutsi testsettets resultat, oppretter vi en y_pred-vektor som vi gjorde i Logistisk regresjon. Nedenfor er koden for det:

Utgang:

Utgangen for ovennevnte kode vil være:

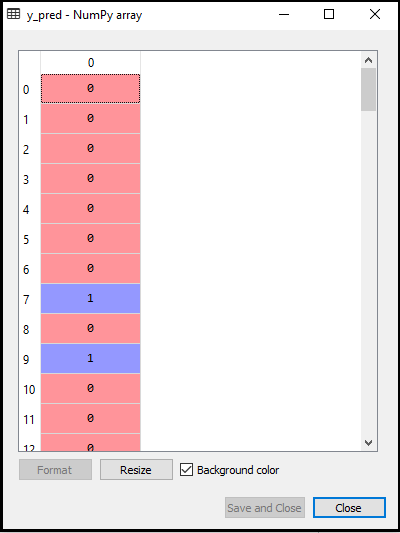
• Opprette forvirringsmatrise:
  Nå oppretter vi forvirringsmatrise for vår K-NN-modell for å se nøyaktigheten til klassifisereren. Nedenfor er koden for det:

I koden ovenfor har vi importert confusion_matrix-funksjonen og kalte den ved hjelp av variabelen cm.

Utgang: Ved å utføre ovennevnte kode, vil vi få matrisen som nedenfor:

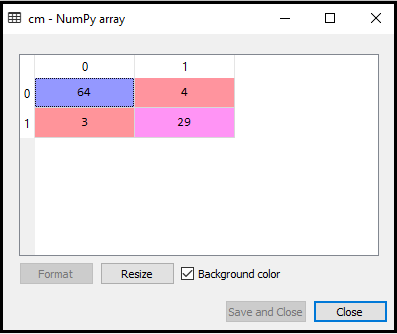
I bildet ovenfor kan vi se det er 64 + 29 = 93 korrekte spådommer og 3 + 4 = 7 feil spådommer, mens det i Logistisk regresjon var 11 feil spådommer. Så vi kan si at ytelsen til modellen forbedres ved å bruke K-NN-algoritmen.

• Visualisering av treningssettresultatet:
  Nå vil vi visualisere treningssettresultatet for K -NN-modell. Koden vil forbli den samme som vi gjorde i Logistic Regression, bortsett fra navnet på grafen. Nedenfor er koden for det:

Output:

Ved å utføre ovennevnte kode, får vi grafen nedenfor:

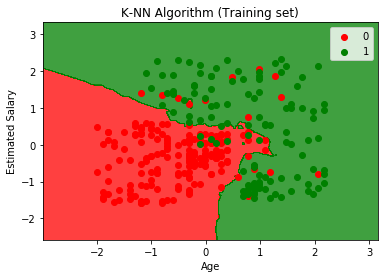
Utgangsgrafen er forskjellig fra grafen som vi har oppstått i Logistisk regresjon. Det kan forstås i punktene nedenfor:

• Som vi kan se, viser grafen det røde punktet og de grønne punktene. De grønne punktene er for kjøpt (1) og røde poeng for ikke kjøpt (0) variabel.
• Grafen viser en uregelmessig grense i stedet for å vise noen rett linje eller en hvilken som helst kurve fordi det er en K-NN-algoritme, dvs. å finne nærmeste nabo.
• Grafen har klassifisert brukere i de riktige kategoriene, ettersom de fleste brukerne som ikke kjøpte SUV er i den røde regionen, og brukere som kjøpte SUV er i den grønne regionen.
• Grafen viser godt resultat, men fremdeles er det noen grønne punkter i den røde regionen og røde punkter i den grønne regionen. Men dette er ikke noe stort problem, da dette modellen forhindres fra å overmontere problemer.
• Derfor er modellen vår godt trent.
• Visualisering av testsettresultatet:
  Etter opplæringen av modellen vil vi nå teste resultatet ved å sette et nytt datasett, dvs. Testdatasett. Koden forblir den samme bortsett fra noen mindre endringer: for eksempel x_train og y_train blir erstattet av x_test og y_test.
  Nedenfor er koden for det:

Utgang:

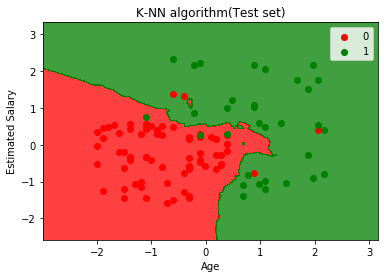
Grafen ovenfor viser utdataene for testdatasettet. Som vi kan se i grafen, er det forventede resultatet godt bra da de fleste av de røde punktene er i den røde regionen og de fleste av de grønne punktene er i det grønne området.

Det er imidlertid få grønne punkter i det røde området og noen få røde punkter i det grønne området. Så dette er feil observasjoner som vi har observert i forvirringsmatrisen (7 Feil utdata).