Kraftberegninger (Norsk)

Force er push or pull.
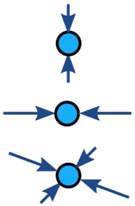
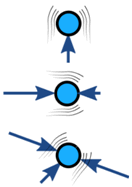
Kreftene på et objekt er vanligvis balansert (hvis ubalansert akselererer objektet):
 |
 |
|
| Balansert | Ubalansert | |
|---|---|---|
| Ingen akselerasjon | Akselerasjon |
Eksempel: Kreftene på toppen av dette brotårnet er i balanse (det akselererer ikke):

Kablene trekkes ned like til venstre og høyre, og det balanseres av tårnet skyver oppover. (Skyver tårnet? Ja! Tenk deg at du står der i stedet for tårnet.)
Vi kan modellere kreftene slik:

Og når vi legg dem head-to-tail vi ser at de lukker seg selv, noe som betyr at nettoeffekten er null:

Kreftene er i balanse.
Styrker i balanse sies å være i likevekt: det er heller ingen endring i bevegelse.
Gratis kroppsdiagrammer
Det første trinnet er å tegne et Free Body Diagram (også kalt et Force Diagram)
Free Body Diagram: En skisse der et legeme kuttes fri fra verden bortsett fra kreftene som virker på det.
I broeksemplet er frikroppsdiagrammet for toppen av tårnet:

Free Body Diagram
Det hjelper oss til å tenke klart om kreftene som virker på kroppen.
Eksempel: Bil på motorvei
Hva er kreftene på en bil som kjører nedover motorveien?

Motoren jobber hardt, så hvorfor fortsetter ikke bilen å akselerere?
Fordi kjøringen kraft balanseres av:
- Luftmotstand (enkelt sagt: th luft motstår å bli presset rundt),
- Rullemotstand, også kalt rullende friksjon (dekkene motstår å ha formen endret)

Free Body Diagram
W er bilens vekt,
R1 og R2 er rullemotstanden til dekkene,
N1 og N2 er reaksjonskreftene (balanserer bilens vekt).
Merk: stålhjul (som på tog) har mindre rullemotstand, men er altfor glatte på veien!
Beregninger
Kraft er en vektor. En vektor har størrelse (størrelse) og retning:

Vi kan modellere kreftene ved å tegne piler av riktig størrelse og retning . Slik:
Eksempel: Beundre utsikten
Brady står på kanten av en balkong støttet av en horisontal bjelke og en stag:

Han veier 80 kg.
Hva er kreftene?
La oss ta det stedet han står på og tenke på kreftene der:

Hans vekt
Hans 80 kg masse skaper en nedadgående kraft på grunn av tyngdekraften.
Kraft er masse ganger akselerasjon: F = ma
Akselerasjonen på grunn av tyngdekraften på jorden er 9,81 m / s2 , så a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
De andre styrkene
Kreftene er balanserte, så de bør lukke seg selv på denne måten:

Vi kan bruke trigonometri for å løse det .
Fordi det er en rettvinklet trekant, vil SOHCAHTOA hjelpe.
For bjelken kjenner vi tilgrensende, vi vil vite motsatt, og «TOA» forteller oss å bruke Tangent:
solbrun (60 ° ) = Stråle / 785 N
Stråle / 785 N = brun (60 °)
Stråle = brun (60 °) × 785 N
Stråle = 1.732 … × 785 N = 1360 N
For Strut, vi kjenner den tilstøtende, vi vil vite hypotenusen, og «CAH» forteller oss å bruke Cosine:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0.5 = 1570 N
Løst:

Interessant hvor mye kraft som er på bjelken og staget sammenlignet med vekten som støttes!
Moment (eller Moment)
Hva om bjelken bare sitter fast i veggen (kalt utkrag)?

Det er ingen støttestøtte, så hva skjer med kreftene?
Free Body Diagram ser slik ut:

Den oppadgående kraften R balanserer vekt nedover.
Med bare de to tvinger bjelken til å spinne som en propell! Men det er også en «dreieeffekt» M kalt Moment (eller Moment) som balanserer den:
Moment: Force ganger avstanden i rette vinkler.
Vi vet at vekten er 785 N, og vi må også vite avstanden i rette vinkler, som i dette tilfellet er 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Og det øyeblikket er det som hindrer at bjelken roterer.

Du kan føle et øyeblikk når du holder på en fiskestang.
I tillegg til å holde vekten, må du forhindre at den roterer nedover.
Friksjon
Rute på en rampe
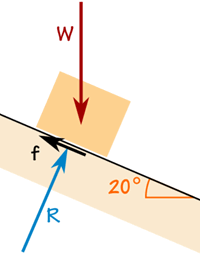
Boksen veier 100 kg.
Friksjonskraften er nok til å holde den der den er.
Reaksjonskraften R er i rett vinkel mot rampe.
Boksen akselererer ikke, så kreftene er i balanse:
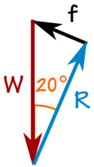
De 100 kg masse skaper en nedadgående kraft på grunn av tyngdekraften:
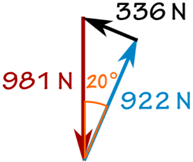
W = 100 kg × 9,81 m / s2 = 981 N
Vi kan bruke SOHCAHTOA til å løse trekanten.
Friksjon f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reaksjon N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Og vi får:
Tips for å tegne gratis kroppsdiagrammer
- Tegn så enkelt som mulig. En boks er ofte god nok.
- Styrker peker i retning de virker på kroppen
- rette piler for krefter
- buede piler for øyeblikk
Sam og Alex Pull a Box
Beregningene kan noen ganger være lettere når vi forvandler størrelse og retning til x og y:
 |
< = > |  |
| Vector a i Polar koordinater |
Vector a i kartesisk koordinater |
Du kan lese hvordan du konverterer dem på Polar og Cartesian Koordinater, men her er et raskt sammendrag:
La oss bruke dem!