MATH 1314: College Algebra (Norsk)
Mens vertikale asymptoter beskriver oppførselen til en graf ettersom utgangen blir veldig stor eller veldig liten, hjelper horisontale asymptoter med å beskrive oppførselen til en graf som inngangen blir veldig stor eller veldig liten. Husk at et polynomets sluttadferd vil speile den som er ledende. Likeledes vil en rasjonell funksjons endemåte speile forholdet mellom de ledende begrepene for teller- og nevnerfunksjonene.
Det er tre forskjellige utfall når du ser etter horisontale asymptoter:
Tilfelle 1: Hvis tellerens grad > tellerens grad, er det en horisontal asymptote ved y = 0.

Tilfelle 2: Hvis graden av nevneren < tellerens grad én, får vi en skrå asymptote.

Legg merke til at mens grafen til en rasjonell funksjon aldri vil krysse en vertikal asymptote, kan grafen kanskje krysse en horisontal eller skrå som ymptote. Selv om grafen til en rasjonell funksjon kan ha mange vertikale asymptoter, vil grafen maksimalt ha en horisontal (eller skrå) asymptote.
Det bør bemerkes at hvis telleren er større enn graden av nevneren med mer enn en, vil sluttatferden til grafen etterligne oppførselen til den reduserte endeadferdsfraksjonen. For eksempel hvis vi hadde funksjonen
med sluttatferd
grafens sluttatferd vil se ut som den til et jevnt polynom med en positiv ledende koeffisient.
En generell merknad: Horisontale asymptoter av rasjonelle funksjoner
Den horisontale asymptoten til en rasjonell funksjon kan være bestemmes ved å se på grader av teller og nevner.
- Tellergrad er mindre enn grad av nevner: horisontal asymptote ved y = 0.
- Tellergrad er større enn grad av nevner med en: ingen horisontal asymptote; skrå asymptote.
- Tellergraden er lik grad av nevner: horisontal asymptote i forholdet mellom ledende koeffisienter.
Eksempel 9: Identifisere horisontale og vertikale asymptoter
Finn de horisontale og vertikale asymptotene til funksjonen
Løsning
Vær først oppmerksom på at denne funksjonen ikke har noen felles faktorer, så det er ingen potensielle fjernbare diskontinuiteter.
Funksjonen vil ha vertikale asymptoter når nevneren er null, noe som får funksjonen til å være udefinert. Nevneren vil være null ved x = 1, -2, tekst {og} 5 \, noe som indikerer vertikale asymptoter ved disse verdiene.
Telleren har grad 2, mens nevneren har grad 3. Siden graden av nevneren er større enn graden av telleren, vil nevneren vokse raskere enn telleren, og føre til at utgangene tenderer mot null når inngangene blir store, og slik som xto pm infty, fleft (xright) til 0 \. Denne funksjonen vil ha en horisontal asymptote ved y = 0 \.
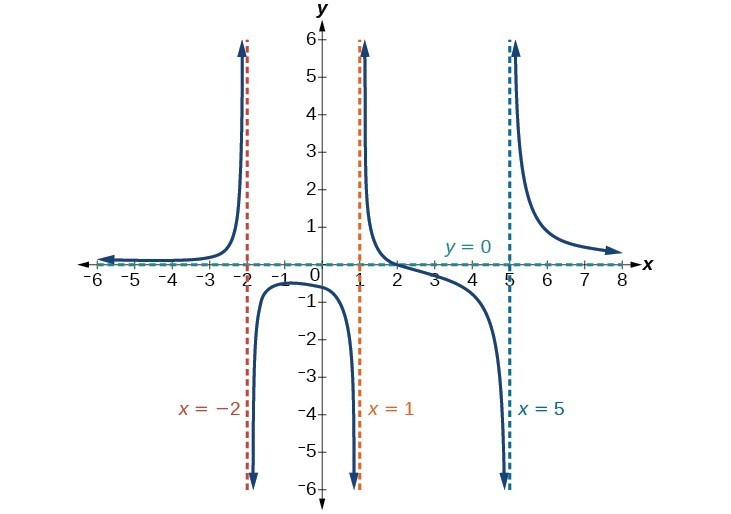
Figur 15
En generell merknad: Avlyttinger av rasjonelle funksjoner
En rasjonell funksjon vil ha et y-skjæringspunkt når inngangen er null, hvis funksjonen er definert til null. En rasjonell funksjon vil ikke ha et y-skjæringspunkt hvis funksjonen ikke er definert ved null.
På samme måte vil en rasjonell funksjon ha x-avskjæringer ved inngangene som får utgangen til å være null. Siden en brøk bare er lik null når telleren er null, kan x-avskjæringer bare forekomme når telleren for den rasjonelle funksjonen er lik null.
Prøv det 7
Gitt den gjensidige kvadratiske funksjonen som er forskjøvet til høyre 3 enheter og ned 4 enheter, skriv dette som en rasjonell funksjon. Finn deretter x– og y-avskjæringer og de horisontale og vertikale asymptotene.
Løsning