For å bestemme fordelingen av en diskret tilfeldig variabel kan vi enten gi dens PMF eller CDF. For kontinuerlige tilfeldige variabler er CDF veldefinert slik at vi kan tilby CDF. PMF fungerer imidlertid ikke for kontinuerlige tilfeldige variabler, fordi for en kontinuerlig tilfeldig variabel $ P (X = x) = 0 $ for alle $ x \ i \ mathbb {R} $. I stedet kan vi vanligvis definere sannsynlighetstetthetsfunksjonen (PDF). PDF-filen er tettheten av sannsynlighet i stedet for sannsynlighetsmasse. Konseptet ligner veldig massetettheten i fysikk: enheten er sannsynlighet per lengdeenhet. For å få en følelse av PDF, bør du vurdere en kontinuerlig tilfeldig variabel $ X $ og definere funksjonen $ f_X (x) $ som følger (uansett hvor grensen eksisterer): $$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P (x

$$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X (x + \ Delta) -F_X (x)} {\ Delta} $$ $$ = \ frac {dF_X (x)} {dx} = F » _X (x), \ hspace {20pt} \ textrm {if} F_X (x) \ textrm {kan differensieres ved} x. $$

Således har vi følgende definisjon for PDF av kontinuerlige tilfeldige variabler:

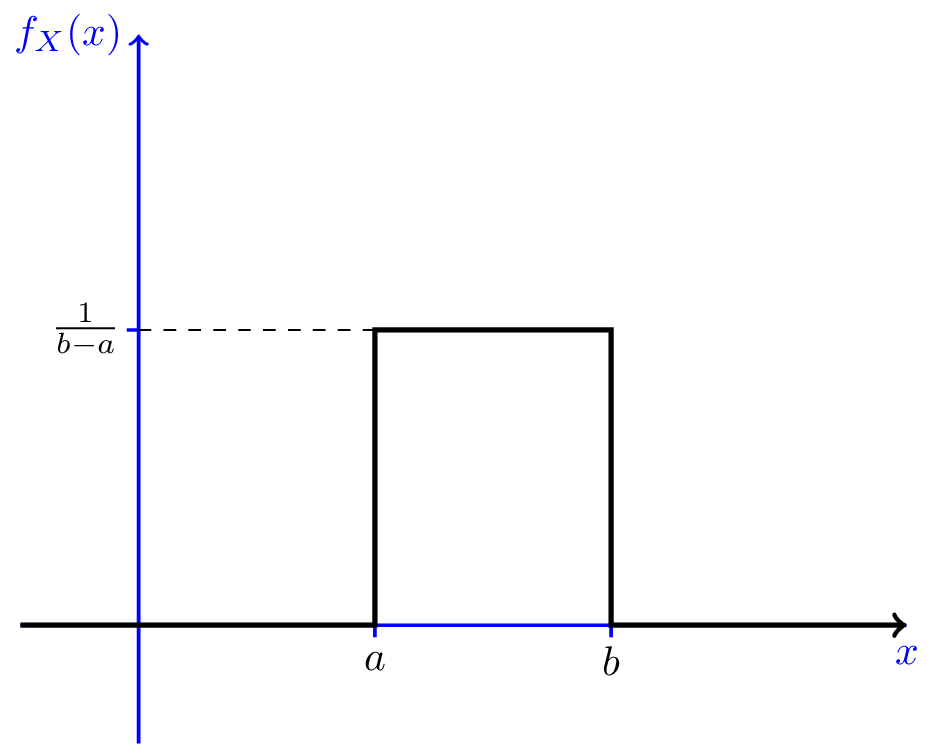
Eksempel
La $ X $ være en kontinuerlig tilfeldig variabel med følgende PDF \ begin {ligning} \ nonumber f_X (x) = \ left \ {\ begin {array} {ll} ce ^ {- x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {ellers} \ end {array} \ høyre. \ end {ligning} hvor $ c $ er en positiv konstant.

1. Finn $ c $.
2. Finn CDF på X, $ F_X (x) $.
3. Finn $ P (1

Rekkevidde