Brattheten i en bakke kalles en skråning. Det samme gjelder brattheten på en linje. Skråningen er definert som forholdet mellom den vertikale endringen mellom to punkter, stigningen, og den horisontale endringen mellom de samme to punktene, løp.

$$ helling = \ frac {rise} {run} = \ frac {endre \: i \: y} {endre \: i \: x} $$

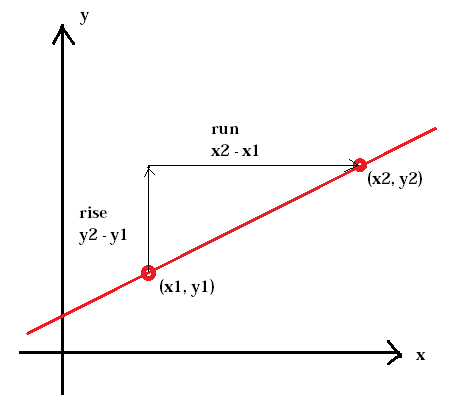
skråningen av en linje er vanligvis representert med bokstaven m. (x1, y1) representerer det første punktet mens (x2, y2) representerer det andre punktet.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Det er viktig å holde x- og y-koordinatene i samme rekkefølge i både teller og nevner ellers får du feil skråning.

Eksempel

Finn skråningen på linjen

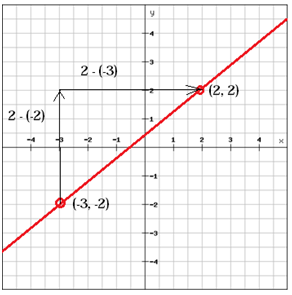
(x1, y1 ) = (-3, -2) og (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

En linje med positiv helling (m > 0), som linjen over, stiger fra venstre til høyre mens en linje med negativ skråning (m < 0) faller fra venstre til høyre.

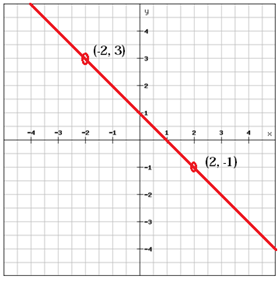
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Hvis to linjer har samme helling, sies det at linjene er p arallel.

Du kan uttrykke en lineær funksjon ved hjelp av skjæringsskjemaet for skråning.

$$ y = mx + b $$

$$ m = helling $ $

$$ b = y – avlyssning $$

Videoleksjon

Finn stigningen