De centrale limietstelling vertelt ons dat naarmate de steekproefomvang groter wordt, de steekproefverdeling van het gemiddelde normaal verdeeld zal worden, zelfs als de gegevens in elk monster niet normaal verdeeld zijn.

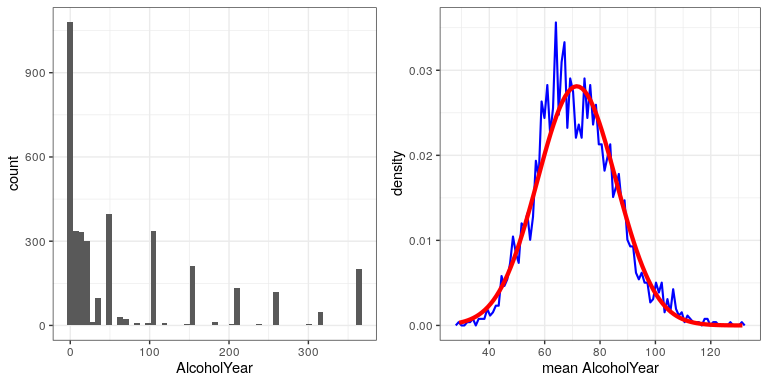
We kunnen dit in echte gegevens zien. Laten we werken met de variabele AlcoholYear in de NHANES-distributie, die sterk scheef is, zoals weergegeven in het linkerpaneel van Afbeelding ??. Deze distributie is, bij gebrek aan een beter woord, funky – en zeker niet normaal verdeeld. Laten we nu eens kijken naar de steekproefverdeling van het gemiddelde voor deze variabele. Figuur 12.2 toont de steekproefverdeling voor deze variabele, die wordt verkregen door herhaaldelijk steekproeven van grootte 50 uit de NHANES-dataset te trekken en het gemiddelde te nemen. Ondanks de duidelijke niet-normaliteit van de oorspronkelijke gegevens, ligt de steekproefverdeling opmerkelijk dicht bij de normale.

De centrale limietstelling is belangrijk voor statistieken omdat het ons in staat stelt veilig aan te nemen dat de steekproefverdeling van het gemiddelde zal in de meeste gevallen normaal zijn. Dit betekent dat we kunnen profiteren van statistische technieken die uitgaan van een normale verdeling, zoals we in de volgende sectie zullen zien.