De steilheid van een heuvel wordt een helling genoemd. Hetzelfde geldt voor de steilheid van een lijn. De helling wordt gedefinieerd als de verhouding van de verticale verandering tussen twee punten, de stijging, en de horizontale verandering tussen dezelfde twee punten, de run.

$$ helling = \ frac {rise} {run} = \ frac {change \: in \: y} {change \: in \: x} $$

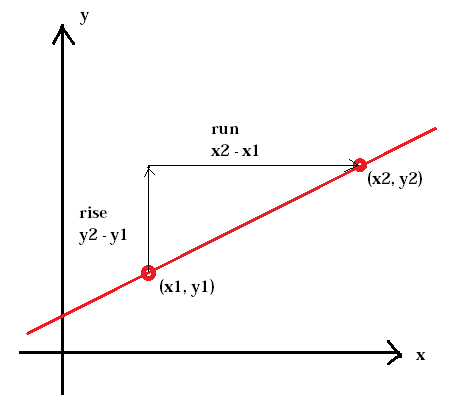
De helling van een lijn wordt meestal weergegeven door de letter m. (x1, y1) vertegenwoordigt het eerste punt terwijl (x2, y2) het tweede punt vertegenwoordigt.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Het is belangrijk om de x- en y-coördinaten in dezelfde volgorde te houden in zowel de teller als de noemer, anders krijg je de verkeerde helling.

Voorbeeld

Vind de helling van de lijn

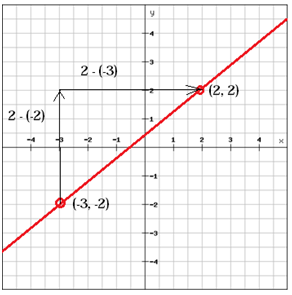
(x1, y1 ) = (-3, -2) en (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Een lijn met een positieve helling (m > 0), zoals de regel hierboven, stijgt van links naar rechts terwijl een lijn met een negatieve helling (m < 0) van links naar rechts valt.

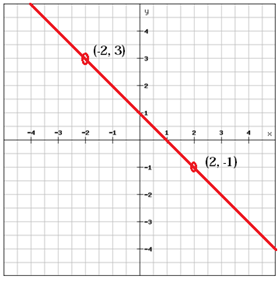
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Als twee lijnen dezelfde helling hebben, wordt gezegd dat ze p zijn arallel.

Je kunt een lineaire functie uitdrukken door gebruik te maken van het hellingsinterceptformulier.

$$ y = mx + b $$

$$ m = helling $ $

$$ b = y – intercept $$

Videolessen

Vind de helling