Forceer berekeningen

Force is push of pull.
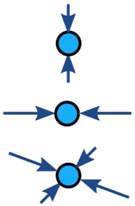
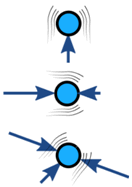
Krachten op een object zijn gewoonlijk gebalanceerd (indien ongebalanceerd versnelt het object):
 |
 |
|
| Gebalanceerd | Ongebalanceerd | |
|---|---|---|
| Geen versnelling | Versnelling |
Voorbeeld: de krachten op de top van deze brugtoren zijn in evenwicht (hij versnelt niet):

De kabels trekken gelijk naar links en rechts naar beneden, en dat wordt gecompenseerd door de opwaartse druk van de toren. (Duwt de toren? Ja! Stel je voor dat je daar staat in plaats van de toren.)
We kunnen de krachten als volgt modelleren:

En wanneer we zet ze kop aan staart dan zien we dat ze zich weer sluiten, wat betekent dat het netto effect nul is:

De krachten zijn in evenwicht.
Krachten in balans zijn in evenwicht: er is ook geen verandering in beweging.
Gratis lichaamsdiagrammen
De eerste stap is om een vrij lichaamsdiagram te tekenen (ook wel een krachtdiagram genoemd)
gratis lichaamsdiagram: een schets waarbij een lichaam wordt losgesneden van de wereld, behalve de krachten die erop inwerken.
In het brugvoorbeeld is het gratis lichaamsdiagram voor de bovenkant van de toren:

Gratis lichaamsdiagram
Het helpt ons helder na te denken over de krachten die op het lichaam inwerken.
Voorbeeld: auto op een snelweg
Wat zijn de krachten op een auto die over de snelweg rijdt?

De motor werkt hard, dus waarom accelereert de auto niet verder?
Omdat het rijden kracht wordt gecompenseerd door:
- Luchtweerstand (simpel gezegd: th De lucht is bestand tegen rondgeduwd worden),
- rolweerstand, ook wel rolweerstand genoemd (de banden zijn bestand tegen het veranderen van vorm)

Gratis carrosseriediagram
W is het gewicht van de auto,
R1 en R2 zijn de rolweerstand van de banden,
N1 en N2 zijn de reactiekrachten (die het gewicht van de auto uitbalanceren).
Let op: stalen wielen (zoals op treinen) hebben minder rolweerstand, maar zijn veel te glad op de weg!
Berekeningen
Kracht is een vector. Een vector heeft magnitude (grootte) en richting:

We kunnen de krachten modelleren door pijlen van de juiste grootte en richting te tekenen . Zo:
Voorbeeld: het uitzicht bewonderen
Brady staat op de rand van een balkon ondersteund door een horizontale balk en een steunbalk:

Hij weegt 80 kg.
Wat zijn de krachten?
Laten we de plek nemen waar hij op staat en nadenken over de krachten die er zijn:

Zijn gewicht
Zijn massa van 80 kg creëert een neerwaartse kracht vanwege de zwaartekracht.
Kracht is massa maal versnelling: F = ma
De versnelling als gevolg van de zwaartekracht op aarde is 9,81 m / s2 , dus a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
The Other Forces
De krachten zijn in evenwicht, dus ze zouden zichzelf als volgt moeten sluiten:

We kunnen trigonometrie gebruiken om het op te lossen .
Omdat het een rechthoekige driehoek is, zal SOHCAHTOA helpen.
Voor de balk kennen we de aangrenzende, we willen het tegenovergestelde weten, en “TOA” vertelt ons dat we Tangent moeten gebruiken:
bruin (60 ° ) = Beam / 785 N
Beam / 785 N = Tan (60 °)
Beam = Tan (60 °) × 785 N
Beam = 1.732 … × 785 N = 1360 N
Voor de Strut kennen we de aangrenzende, we willen de hypotenusa weten, en “CAH” vertelt ons om Cosinus te gebruiken:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0.5 = 1570 N
Opgelost:

Interessant hoeveel kracht er is de balk en steun in vergelijking met het gewicht dat wordt ondersteund!
Koppel (of moment)
Wat als de balk gewoon in de muur wordt geplakt (een cantilever genoemd)?

Er is geen steunpilaar, dus wat gebeurt er met de krachten?
Het Free Body Diagram ziet er als volgt uit:

De opwaartse kracht R compenseert het neerwaartse gewicht.
Met alleen die twee krachten die de straal zal draaien als een propeller! Maar er is ook een ‘draaiend effect’ M genaamd Moment (of Koppel) dat het in evenwicht brengt:
Moment: kracht maal de afstand in rechte hoeken.
We weten dat het gewicht is 785 N, en we moeten ook de afstand in rechte hoeken weten, die in dit geval 3,2 m is.
M = 785 N x 3,2 m = 2512 Nm
En dat moment is wat de straal stopt met draaien.

U kunt een moment voelen wanneer u zich aan een hengel vasthoudt.
Naast het vasthouden van het gewicht, moet u voorkomen dat het naar beneden draait.
Wrijving
Box op een helling
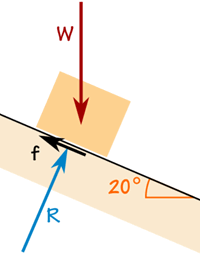
De kist weegt 100 kg.
De wrijvingskracht is voldoende om hem op zijn plek te houden.
De reactiekracht R staat haaks op de oprit.
De box accelereert niet, dus de krachten zijn in balans:
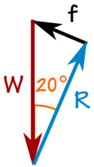
De 100 kg massa creëert een neerwaartse kracht als gevolg van zwaartekracht:
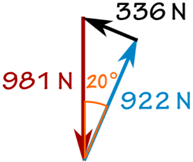
W = 100 kg × 9,81 m / s2 = 981 N
We kunnen SOHCAHTOA gebruiken om de driehoek op te lossen.
Wrijving f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reactie N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
En we krijgen:
Tips voor het tekenen van vrije lichaamsdiagrammen
- Teken zo eenvoudig mogelijk. Een doos is vaak goed genoeg.
- Krachten wijzen in de richting waarin ze inwerken op het lichaam
- rechte pijlen voor krachten
- gebogen pijlen voor momenten
Sam en Alex trekken aan een doos
De berekeningen kunnen soms gemakkelijker zijn als we grootte en richting omzetten in x en y:
 |
< = > |  |
| Vector a in polaire coördinaten |
Vector a in Cartesiaans Coördinaten |
Je kunt lezen hoe je ze converteert in Polar en Cartesiaans Coördinaten, maar hier is een korte samenvatting:
Laten we ze gebruiken!