Parametrische en niet-parametrische tests voor het vergelijken van twee of meer groepen

Statistieken: parametrische en niet-parametrische tests

Deze sectie omvat:

• Een test kiezen
• Parametrische tests
• Niet-parametrische tests

Een test kiezen

In termen van het selecteren van een statistische toets, is de belangrijkste vraag “wat is de belangrijkste studiehypothese?” In sommige gevallen is er geen hypothese; de onderzoeker wil gewoon “zien wat er is”. In een prevalentieonderzoek is er bijvoorbeeld geen hypothese om te testen, en de omvang van het onderzoek wordt bepaald door hoe nauwkeurig de onderzoeker de prevalentie wil bepalen. Als er geen hypothese is, is er geen statistische test. Het is belangrijk om a priori te beslissen welke hypotheses bevestigend zijn (dat wil zeggen, een veronderstelde relatie testen) en welke verkennend zijn (worden gesuggereerd door de gegevens). Geen enkele studie kan een hele reeks hypothesen ondersteunen. Een verstandig plan is om het aantal bevestigende hypothesen ernstig te beperken. Hoewel het geldig is om statistische tests te gebruiken op hypothesen die door de gegevens worden gesuggereerd, mogen de P-waarden alleen als richtlijn worden gebruikt en mogen de resultaten als voorlopig worden behandeld totdat ze door daaropvolgende onderzoeken worden bevestigd. Een handige gids is om een Bonferroni-correctie te gebruiken, die eenvoudig stelt dat als men n onafhankelijke hypothesen test, men een significantieniveau van 0,05 / n moet gebruiken. Dus als er twee onafhankelijke hypothesen zouden zijn, zou een resultaat alleen significant worden verklaard als P < 0,025. Merk op dat, aangezien tests zelden onafhankelijk zijn, dit een zeer conservatieve procedure is – d.w.z. een procedure die de nulhypothese waarschijnlijk niet verwerpt. De onderzoeker moet dan vragen “zijn de gegevens onafhankelijk?” Dit kan moeilijk te beslissen zijn, maar als vuistregel zijn resultaten voor hetzelfde individu of van gematchte individuen niet onafhankelijk. De resultaten van een crossover-studie of van een case-control-studie waarin de controles werden vergeleken met de gevallen op basis van leeftijd, geslacht en sociale klasse, zijn dus niet onafhankelijk.

• Analyse moet het ontwerp weerspiegelen , en daarom moet een passend ontwerp worden gevolgd door een passende analyse.
• Resultaten die in de loop van de tijd worden gemeten, vereisen speciale zorg. Een van de meest voorkomende fouten bij statistische analyse is om gecorreleerde variabelen
  onafhankelijk te behandelen. Stel dat we kijken naar de behandeling van beenulcera, waarbij sommige mensen een maagzweer op elk been hadden. We hebben misschien 20 proefpersonen met
  30 zweren, maar het aantal onafhankelijke stukjes informatie is 20 omdat de toestand van zweren op elk been voor één persoon kan worden beïnvloed door de
  gezondheidstoestand van de persoon en een analyse die zweren beschouwen als onafhankelijke waarnemingen zouden onjuist zijn. Raadpleeg een statisticus voor een correcte analyse van gemengde gepaarde en ongepaarde gegevens.

De volgende vraag is “welke soorten gegevens worden gemeten?” De gebruikte test moet worden bepaald door de gegevens. De keuze van de test voor gematchte of gepaarde gegevens wordt beschreven in Tabel 1 en voor onafhankelijke gegevens in Tabel 2.

Tabel 1 Keuze van statistische test uit gepaarde of gematchte observatie

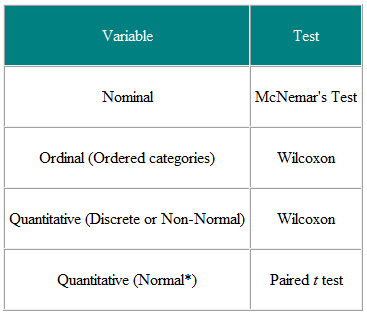
Het is handig om de invoervariabelen en de uitkomstvariabelen te bepalen. In een klinische proef is de inputvariabele bijvoorbeeld het type behandeling – een nominale variabele – en het resultaat kan een klinische maat zijn, misschien normaal verdeeld. De vereiste test is dan de t-test (tabel 2). Als de invoervariabele echter continu is, bijvoorbeeld een klinische score, en de uitkomst is nominaal, zeg maar genezen of niet genezen, is logistische regressie de vereiste analyse. Een t-test kan in dit geval helpen, maar zou ons niet geven wat we nodig hebben, namelijk de waarschijnlijkheid van genezing voor een bepaalde waarde van de klinische score. Als een ander voorbeeld, stel dat we een cross-sectioneel onderzoek hebben waarin we een willekeurige steekproef van mensen vragen of ze denken dat hun huisarts het goed doet, op een vijfpuntsschaal, en we willen nagaan of vrouwen een hogere mening hebben. van huisartsen dan mannen. De invoervariabele is geslacht, wat nominaal is. De uitkomstvariabele is de ordinale schaal met vijf punten. De mening van elke persoon is onafhankelijk van de anderen, dus we hebben onafhankelijke gegevens. Uit tabel 2 moeten we een χ2-test gebruiken voor trend, of een Mann-Whitney U-test met een correctie voor gelijkspel (NB een gelijkspel treedt op wanneer twee of meer waarden zijn hetzelfde, dus er is geen strikt stijgende rangorde – waar dit gebeurt, kan men het gemiddelde van de rangorde maken voor gelijke waarden.) Merk echter op dat als sommige mensen een huisarts delen en anderen niet, dan zijn de gegevens niet onafhankelijke en een meer geavanceerde analyse is vereist. Merk op dat deze tabellen alleen als richtlijnen moeten worden beschouwd en dat elk geval op zijn merites moet worden bekeken.

Tabel 2 Keuze van statistische test voor onafhankelijke waarnemingen

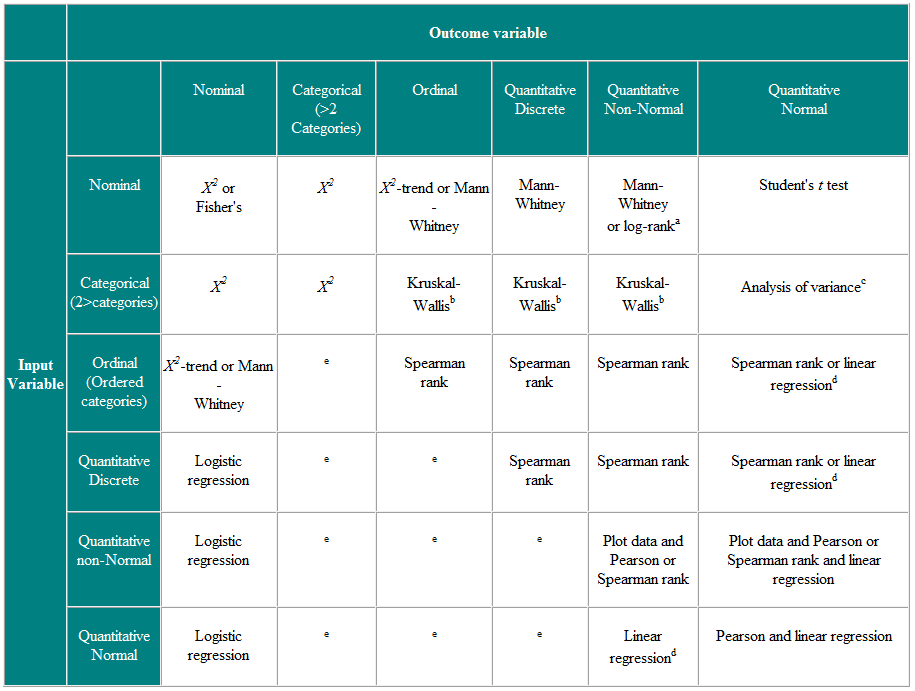
a Als gegevens worden gecensureerd. b De Kruskal-Wallis-test wordt gebruikt voor het vergelijken van ordinale of niet-normale variabelen voor meer dan twee groepen, en is een generalisatie van de Mann-Whitney U-test. c Variantieanalyse is een algemene techniek en één versie (eenrichtingsvariantieanalyse) wordt gebruikt om normaal verdeelde variabelen voor meer dan twee groepen te vergelijken, en is het parametrische equivalent van de Kruskal-Wallistest. d Als de uitkomstvariabele de afhankelijke variabele is, dan is op voorwaarde dat de residuen (de verschillen tussen de waargenomen waarden en de voorspelde respons van regressie) plausibel zijn. Normaal verdeeld, dan is de verdeling van de onafhankelijke variabele niet belangrijk. e Er zijn een aantal meer geavanceerde technieken, zoals Poisson-regressie, om met deze situaties om te gaan. Ze vereisen echter bepaalde aannames en het is vaak gemakkelijker om de uitkomstvariabele te dichotomiseren of als continu te behandelen.

Parametrische tests zijn tests die aannames doen over de parameters van de populatieverdeling waaruit de steekproef wordt getrokken. . Dit is vaak de aanname dat de populatiegegevens normaal verdeeld zijn. Niet-parametrische tests zijn “distributievrij” en kunnen als zodanig worden gebruikt voor niet-normale variabelen. Tabel 3 toont het niet-parametrische equivalent van een aantal parametrische tests.

Tabel 3 Parametrische en Niet-parametrische tests voor het vergelijken van twee of meer groepen

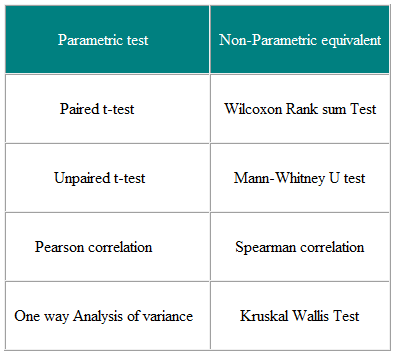
Niet-parametrische tests zijn geldig voor zowel niet-normaal verdeelde gegevens als Normaal gedistribueerde gegevens, dus waarom zou u ze niet altijd gebruiken?

Het lijkt verstandig om in alle gevallen niet-parametrische tests te gebruiken, waardoor u niet hoeft te testen op Normality. Parametrische tests hebben de voorkeur, echter, om de volgende redenen:

1. We zijn zelden geïnteresseerd in alleen een significantietest; we willen graag iets zeggen over de populatie waaruit de steekproeven afkomstig zijn, en dit kan het beste worden gedaan met
schattingen van parameters en betrouwbaarheidsintervallen.

2. Het is moeilijk om flexibel te modelleren met niet-parametrische tests, bijvoorbeeld om verstorende factoren toe te staan met behulp van meerdere regressie.

3. Parametrische tests hebben meestal meer statistische kracht dan hun niet-parametrische equivalenten. Met andere woorden, de kans is groter dat significante verschillen

bestaan.

Vergelijken niet-parametrische tests medianen?

Het is algemeen aangenomen dat een Mann-Whitney U-test is in feite een test voor verschillen in medianen. Twee groepen kunnen echter dezelfde mediaan hebben en toch een significante Mann-Whitney U-test hebben. Beschouw de volgende gegevens voor twee groepen, elk met 100 waarnemingen. Groep 1:98 (0), 1, 2; Groep 2:51 (0), 1, 48 (2). De mediaan is in beide gevallen 0, maar van de Mann-Whitney-test P < 0.0001. Alleen als we bereid zijn om de aanvullende aanname te maken dat het verschil tussen de twee groepen simpelweg een locatieverschuiving is (dat wil zeggen, de verdeling van de gegevens in de ene groep wordt eenvoudigweg met een vast bedrag verschoven ten opzichte van de andere), kunnen we zeggen dat de test is een test van het verschil in medianen. Als de groepen echter dezelfde verdeling hebben, zal een verschuiving in locatie medianen en gemiddelden met dezelfde hoeveelheid verplaatsen en dus is het verschil in medianen hetzelfde als het verschil in gemiddelden. De Mann-Whitney U-test is dus ook een test voor het verschil in gemiddelden. Hoe is de Mann-Whitney U-test gerelateerd aan de t-test? Als iemand de gegevens in plaats van de gegevens zelf zou invoeren in een twee-steekproefprogramma voor t-testen, zou de verkregen P-waarde zeer dicht bij die van een Mann-Whitney U-test liggen.