Centralne twierdzenie graniczne mówi nam, że wraz ze wzrostem wielkości próby rozkład średniej będzie miał rozkład normalny, nawet jeśli dane w każdej próbce nie mają rozkładu normalnego.

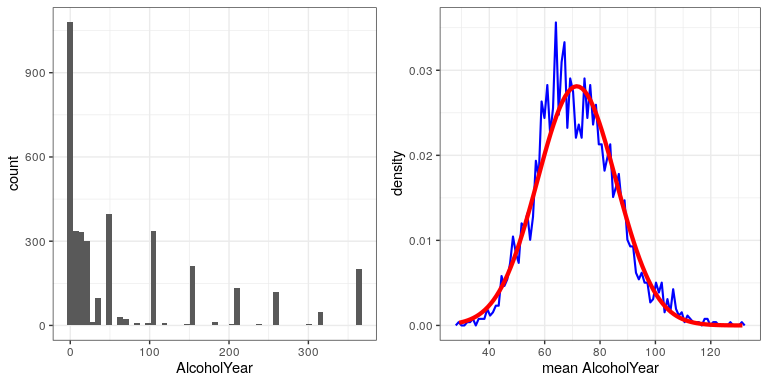
Widzimy to w rzeczywistych danych. Popracujmy ze zmienną AlcoholYear w rozkładzie NHANES, która jest mocno wypaczona, jak pokazano na lewym panelu rysunku ??. Ta dystrybucja jest, z braku lepszego słowa, funky – i zdecydowanie nie jest dystrybuowana normalnie. Przyjrzyjmy się teraz rozkładowi próbkowania średniej dla tej zmiennej. Rysunek 12.2 przedstawia rozkład próbkowania dla tej zmiennej, który uzyskuje się poprzez wielokrotne pobieranie próbek o rozmiarze 50 ze zbioru danych NHANES i pobieranie średniej. Pomimo wyraźnej nienormalności oryginalnych danych, rozkład próbkowania jest bardzo zbliżony do normalnego.

Centralne twierdzenie graniczne jest ważne dla statystyki, ponieważ pozwala nam bezpiecznie założyć, że w większości przypadków rozkład średniej z próby będzie normalny. Oznacza to, że możemy skorzystać z technik statystycznych, które zakładają rozkład normalny, co zobaczymy w następnej sekcji.