• K-Nearest Neighbor to jeden z najprostszych algorytmów uczenia maszynowego o technice nadzorowanego uczenia się.
• Algorytm K-NN zakłada podobieństwo między nowym przypadkiem / danymi a dostępnymi przypadkami i umieszcza nowy przypadek w kategorii najbardziej podobnej do dostępnych kategorii.

K-NN przechowuje wszystkie dostępne dane i klasyfikuje nowy punkt danych na podstawie podobieństwa. Oznacza to, że gdy pojawiają się nowe dane, można je łatwo zaklasyfikować do kategorii zestawu dobrze za pomocą algorytmu K-NN.

• Algorytm K-NN może być używany zarówno do regresji, jak i do klasyfikacji, ale głównie jest używany do rozwiązywania problemów klasyfikacyjnych.
• K-NN jest algorytmem nieparametrycznym, co oznacza nie przyjmuje żadnych założeń na podstawie danych.
• Jest również nazywany algorytmem leniwego ucznia, ponieważ nie uczy się od razu z zestawu uczącego, zamiast tego przechowuje zestaw danych i podczas klasyfikacji wykonuje działanie na zbiorze danych.
• Algorytm KNN w fazie uczenia po prostu przechowuje zbiór danych, a kiedy otrzymuje nowe dane, klasyfikuje je do kategorii, która jest bardzo podobna do nowych danych.
• Przykład: Załóżmy, że mamy obraz stworzenia, które wygląda podobnie do kota i psa, ale chcemy wiedzieć, czy jest to kot, czy pies. Więc do tej identyfikacji możemy użyć algorytmu KNN, ponieważ działa on na mierze podobieństwa. Nasz model KNN znajdzie podobne cechy nowego zestawu danych do obrazów kotów i psów i na podstawie najbardziej podobnych funkcji umieści go w kategorii kot lub pies.

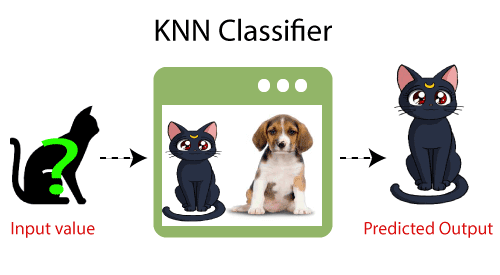
Dlaczego potrzebujemy algorytmu K-NN?

Załóżmy, że istnieją dwie kategorie, tj. Kategoria A i Kategoria B, i mamy nowy punkt danych x1, więc ten punkt danych będzie znajdować się w której z tych kategorii. Aby rozwiązać tego typu problem, potrzebujemy algorytmu K-NN. Z pomocą K-NN możemy łatwo zidentyfikować kategorię lub klasę określonego zbioru danych. Rozważ poniższy diagram:

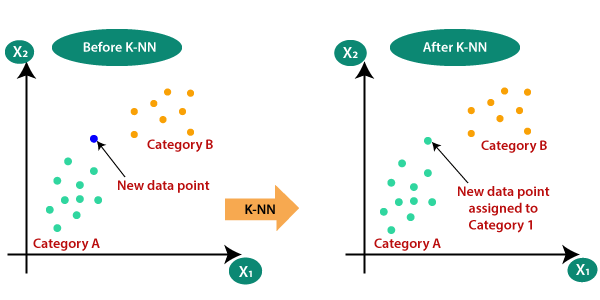
Jak działa K-NN?

Działanie K-NN można wyjaśnić na podstawie poniższy algorytm:

• Krok 1: Wybierz liczbę K sąsiadów
• Krok 2: Oblicz odległość euklidesową K liczby sąsiadów
• Krok-3: Weź K najbliższych sąsiadów zgodnie z obliczoną odległością euklidesową.
• Krok-4: Wśród tych k sąsiadów policz liczbę punktów danych w każdej kategorii.
• Krok 5: przypisz nowe punkty danych do tej kategorii, dla której liczba sąsiadów jest maksymalna.
• Krok-6: Nasz model jest gotowy.

Załóżmy, że mamy nowy punkt danych i musimy umieścić go w wymaganej kategorii. Rozważ poniższy obrazek:

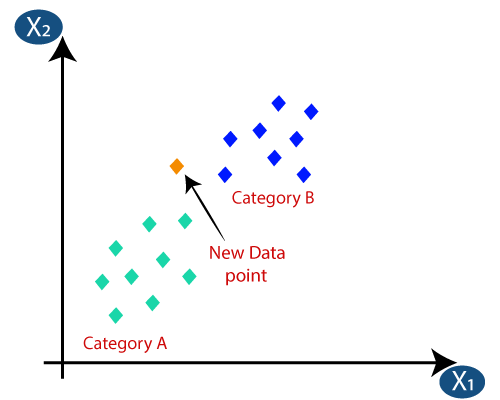
• Najpierw wybierzemy liczbę sąsiadów, więc wybierzemy k = 5.
• Następnie obliczymy odległość euklidesową między punktami danych. Odległość euklidesowa to odległość między dwoma punktami, którą już badaliśmy w geometrii. Można ją obliczyć w następujący sposób:

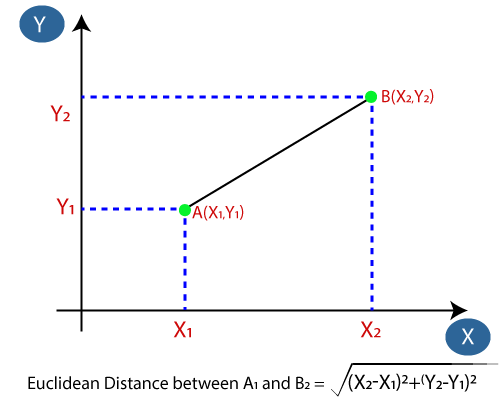
• Obliczając odległość euklidesową, otrzymaliśmy najbliższych sąsiadów, jako trzech najbliższych sąsiadów w kategorii A i dwóch najbliższych sąsiadów w kategorii B. Rozważ poniższy obraz:

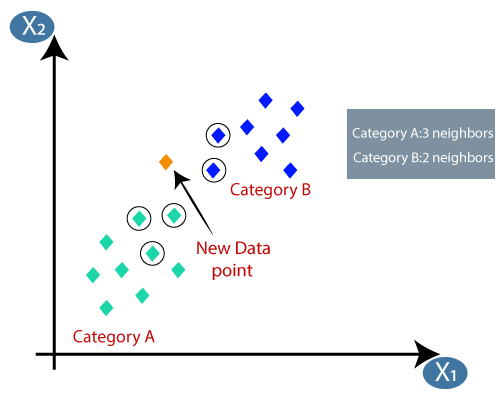
• Jak widać, 3 najbliższych sąsiadów pochodzi z kategorii A, stąd ten nowy punkt danych musi należeć do kategorii A.

Jak wybrać wartość K w algorytmie K-NN?

Poniżej znajduje się kilka punktów do pamiętaj wybierając wartość K w algorytmie K-NN:

• Nie ma konkretnego sposobu na określenie najlepszej wartości dla „K”, więc musimy wypróbować kilka wartości, aby znaleźć najlepszą z nich. Najbardziej preferowaną wartością K jest 5.
• Bardzo niska wartość K, na przykład K = 1 lub K = 2, może być zaszumiona i prowadzić do efektów odstających w modelu.
• Duże wartości K są dobre, ale mogą sprawiać pewne trudności.

Zalety algorytmu KNN:

• Jest prosty w implementacji.
• Jest odporny na zaszumione dane uczące
• Może być bardziej efektywny, jeśli dane uczące są duże.

Wady algorytmu KNN:

• Zawsze trzeba określić wartość K, która może być przez jakiś czas skomplikowana.
• Koszt obliczeń jest wysoki ze względu na obliczenie odległości między punktami danych dla wszystkich próbek uczących .

Implementacja algorytmu KNN w Pythonie

Aby wykonać implementację algorytmu K-NN w języku Python, użyjemy tego samego problemu i zbioru danych, których używaliśmy w Regresja logistyczna. Ale tutaj poprawimy wydajność modelu. Poniżej znajduje się opis problemu:

Problem dotyczący algorytmu K-NN: Istnieje firma produkująca samochody, która wyprodukowała nowy samochód typu SUV.Firma chce wyświetlać reklamy użytkownikom, którzy są zainteresowani zakupem tego SUV-a. Dlatego w przypadku tego problemu mamy zbiór danych, który zawiera informacje o wielu użytkownikach za pośrednictwem sieci społecznościowej. Zbiór danych zawiera wiele informacji, ale szacunkowe wynagrodzenie i wiek, które uwzględnimy dla zmiennej niezależnej, a zmienna Zakup dotyczy zmiennej zależnej. Poniżej znajduje się zbiór danych:

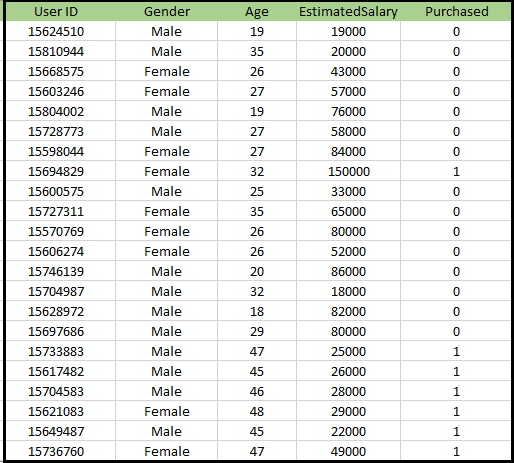
Kroki do zaimplementowania algorytmu K-NN:

• Etap wstępnego przetwarzania danych
• Dopasowanie algorytmu K-NN do zbioru uczącego
• Przewidywanie wyniku testu
• Dokładność testu wyniku (macierz tworzenia pomyłek)
• Wizualizacja wyniku zestawu testowego.

Krok wstępnego przetwarzania danych:

Krok wstępnego przetwarzania danych pozostanie dokładnie taki sam jak regresja logistyczna. Poniżej znajduje się kod za to:

Wykonując powyższy kod, nasz zbiór danych jest importowany do naszego programu i dobrze wstępnie przetworzony. Po skalowaniu funkcji nasz testowy zestaw danych będzie wyglądał następująco:

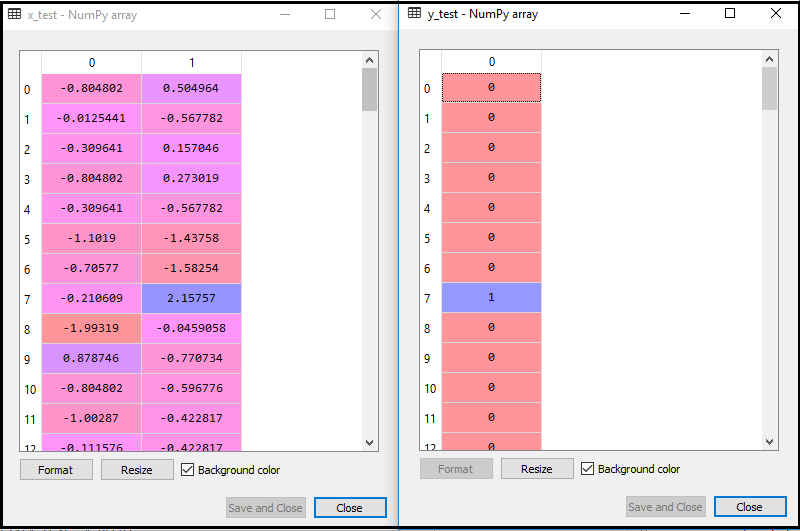
Z powyższego wyjścia im wieku, widzimy, że nasze dane zostały pomyślnie przeskalowane.

• Dopasowanie klasyfikatora K-NN do danych uczących:
  Teraz dopasujemy klasyfikator K-NN do danych uczących. W tym celu zaimportujemy klasę KNeighborsClassifier z biblioteki Sklearn Neighbors. Po zaimportowaniu klasy utworzymy obiekt Classifier tej klasy. Parametrem tej klasy będzie
  • n_neighbors: Aby zdefiniować wymaganych sąsiadów algorytmu. Zwykle zajmuje to 5.
  • metric = „minkowski”: To jest parametr domyślny i decyduje o odległości między punktami.
  • p = 2: Jest to odpowiednik standardu Metryka euklidesowa.

  Następnie dopasujemy klasyfikator do danych uczących. Poniżej znajduje się odpowiedni kod:

Wynik: Wykonując powyższy kod, otrzymamy wynik w postaci:

• Przewidywanie wyniku testu: Aby przewidzieć wynik testu, utworzymy wektor y_pred, tak jak zrobiliśmy to w regresji logistycznej. Poniżej znajduje się odpowiedni kod:

Dane wyjściowe:

Dane wyjściowe dla powyższego kodu będą wyglądać następująco:

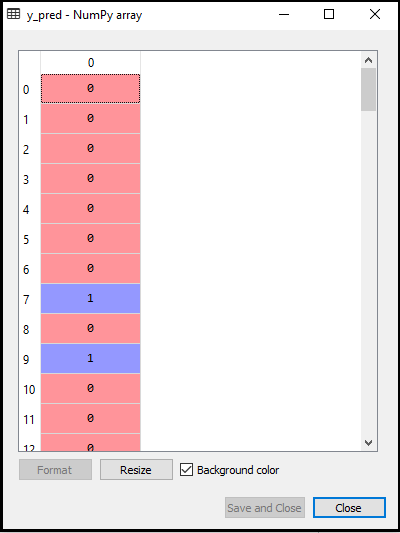
• Tworzenie macierzy nieporozumień:
  Teraz utworzymy macierz nieporozumień dla naszego modelu K-NN, aby zobaczyć dokładność klasyfikatora. Poniżej znajduje się jej kod:

W powyższym kodzie zaimportowaliśmy funkcję confusion_matrix i nazwaliśmy ją za pomocą zmiennej cm.

Wynik: Wykonując powyższy kod, otrzymamy macierz jak poniżej:

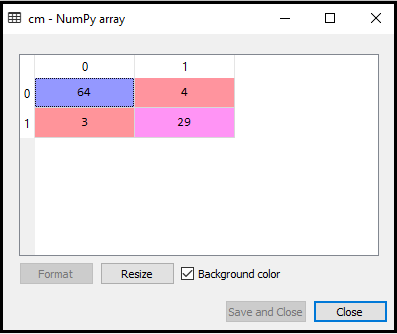
Na powyższym obrazku widzimy jest 64 + 29 = 93 poprawnych prognoz i 3 + 4 = 7 błędnych prognoz, podczas gdy w regresji logistycznej było 11 błędnych prognoz. Możemy więc powiedzieć, że wydajność modelu jest poprawiona przy użyciu algorytmu K-NN.

• Wizualizacja wyniku zbioru uczącego:
  Teraz zwizualizujemy wynik zbioru uczącego dla K -NN model. Kod pozostanie taki sam, jak w przypadku regresji logistycznej, z wyjątkiem nazwy wykresu. Poniżej znajduje się odpowiedni kod:

Wyjście:

Wykonując powyższy kod, otrzymamy poniższy wykres:

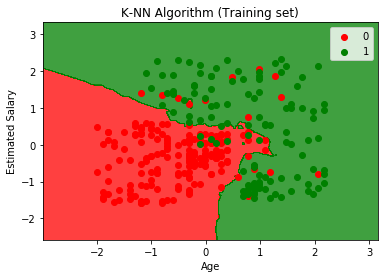
Wykres wyjściowy różni się od wykresu, który wystąpił w regresji logistycznej. Można to zrozumieć w poniższych punktach:

• Jak widzimy, wykres przedstawia czerwony punkt i zielone punkty. Zielone punkty są za zmienną Zakupione (1), a Czerwone Punkty za zmienną nie zakupione (0).
• Wykres pokazuje nieregularną granicę zamiast pokazywać linię prostą lub jakąkolwiek krzywą, ponieważ jest to algorytm K-NN, tj. znajdujący najbliższego sąsiada.
• Na wykresie sklasyfikowano użytkowników we właściwych kategoriach, ponieważ większość użytkowników, którzy nie kupili SUV-a, znajduje się w regionie czerwonym, a użytkownicy, którzy kupili SUVa, w regionie zielonym.
• Wykres pokazuje dobry wynik, ale nadal są zielone punkty w czerwonym obszarze i czerwone punkty w zielonym. Ale to nie jest duży problem, ponieważ wykonanie tego modelu zapobiega problemom z nadmiernym dopasowaniem.
• Dlatego nasz model jest dobrze wyszkolony.
• Wizualizacja wyniku zestawu testowego:
  Po uczeniu modelu przetestujemy teraz wynik, umieszczając nowy zestaw danych, tj. Testowy zestaw danych. Kod pozostaje taki sam, z wyjątkiem kilku drobnych zmian: na przykład x_train i y_train zostaną zastąpione przez x_test i y_test.
  Poniżej znajduje się odpowiadający mu kod:

Dane wyjściowe:

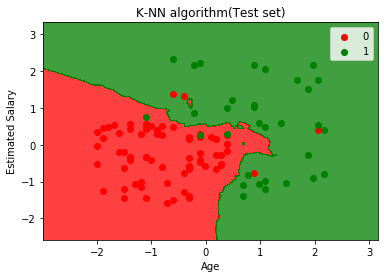
Powyższy wykres przedstawia dane wyjściowe dla zestawu danych testowych. Jak widać na wykresie, przewidywane wyniki są dobrze dobrze, ponieważ większość czerwonych punktów znajduje się w czerwonym obszarze i większość zielonych punktów znajduje się w zielonym regionie.

Jednak jest kilka zielonych punktów w czerwonym obszarze i kilka czerwonych punktów w zielonym. Więc są to niepoprawne obserwacje, które zaobserwowaliśmy w macierzy pomyłki (7 Niepoprawne dane wyjściowe).