MATH 1314: College Algebra (Polski)
Podczas gdy pionowe asymptoty opisują zachowanie wykresu, gdy wynik staje się bardzo duży lub bardzo mały, poziome asymptoty pomagają opisać zachowanie wykresu jako wejście staje się bardzo duże lub bardzo małe. Przypomnij sobie, że końcowe zachowanie wielomianu będzie odzwierciedlać zachowanie terminu wiodącego. Podobnie, końcowe zachowanie funkcji wymiernej będzie odzwierciedlać stosunek wiodących składników funkcji licznika i mianownika.
Podczas sprawdzania asymptot poziomych występują trzy różne wyniki:
Przypadek 1: Jeśli stopień mianownika > stopień licznika, występuje pozioma asymptota w miejscu y = 0.

Przypadek 2: Jeśli stopień mianownika < stopień licznika o jeden, otrzymamy asymptotę skośną.

Zauważ, że chociaż wykres funkcji wymiernej nigdy nie przecina pionowej asymptoty, wykres może, ale nie musi, przecinać poziomą lub skośną ymptote. Ponadto, chociaż wykres funkcji wymiernej może mieć wiele asymptot pionowych, wykres będzie miał co najwyżej jedną asymptotę poziomą (lub skośną).
Należy zauważyć, że jeśli stopień licznika jest większy niż stopień mianownika o więcej niż jeden, końcowe zachowanie wykresu będzie naśladować zachowanie zredukowanej części zachowania końcowego. Na przykład, gdybyśmy mieli funkcję
z zachowaniem końcowym
końcowe zachowanie wykresu byłoby podobne do zachowania parzystego wielomianu z dodatnim współczynnikiem wiodącym.
Uwaga ogólna: poziome asymptoty funkcji wymiernych
Poziomą asymptotą funkcji wymiernej można określane na podstawie stopni licznika i mianownika.
- Stopień licznika jest mniejszy niż stopień mianownika: pozioma asymptota przy y = 0.
- Stopień licznika to większy niż stopień mianownika o jeden: brak asymptoty poziomej; asymptota skośna.
- Stopień licznika jest równy stopniowi mianownika: asymptota pozioma przy stosunku współczynników wiodących.
Przykład 9: Identyfikacja poziomych i pionowych asymptot
Znajdź poziome i pionowe asymptoty funkcji
Rozwiązanie
Po pierwsze, zauważ, że ta funkcja nie ma wspólnych czynników, więc nie ma żadnych możliwych do usunięcia nieciągłości.
Funkcja będzie miała pionowe asymptoty, gdy mianownik będzie równy zero, co spowoduje, że funkcja będzie niezdefiniowana. Mianownik będzie wynosił zero przy x = 1, -2, text {i} 5 \, wskazując pionowe asymptoty przy tych wartościach.
Licznik ma stopień 2, podczas gdy mianownik ma stopień 3. Ponieważ stopień mianownika jest większa niż stopień licznika, mianownik będzie rósł szybciej niż licznik, powodując tendencję wyjściową do zera, gdy nakłady stają się duże, a więc xto pm infty, fleft (xright) do 0 \. Ta funkcja będzie miała asymptotę poziomą w miejscu y = 0 \.
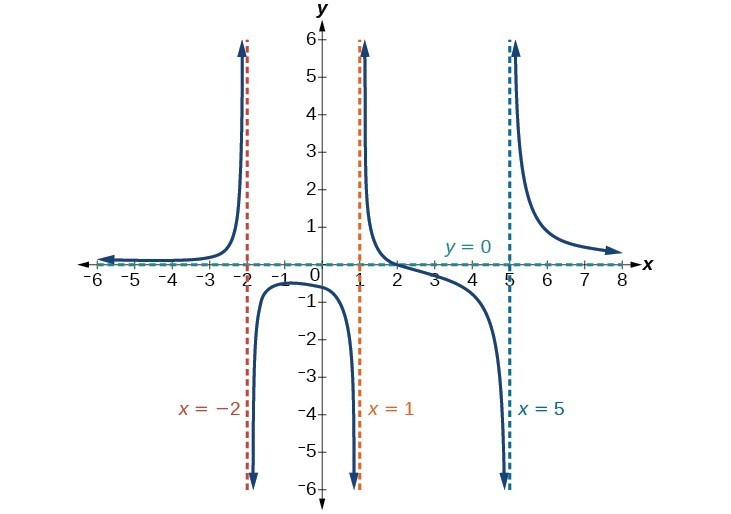
Rysunek 15
Ogólna uwaga: punkty przecięcia funkcji wymiernych
Funkcja wymierna będzie miała punkt przecięcia z osią y, gdy dane wejściowe są zero, jeśli funkcja jest zdefiniowana jako zero. Funkcja wymierna nie będzie miała punktu przecięcia z osią y, jeśli funkcja nie jest zdefiniowana jako zero.
Podobnie funkcja wymierna będzie miała punkty przecięcia z osią x na wejściach, które spowodują, że na wyjściu będzie zero. Ponieważ ułamek jest równy zero tylko wtedy, gdy licznik jest równy zero, przecięcia z osią x mogą wystąpić tylko wtedy, gdy licznik funkcji wymiernej jest równy zero.
Spróbuj 7
Biorąc pod uwagę funkcję odwrotności do kwadratu, która jest przesunięta w prawo o 3 jednostki i w dół o 4 jednostki, zapisz to jako funkcję wymierną. Następnie znajdź punkty przecięcia z osiami x– i y oraz asymptoty poziome i pionowe.
Rozwiązanie