Nachylenie wzgórza nazywa się zboczem. To samo dotyczy stromości linii. Nachylenie definiuje się jako stosunek pionowej zmiany między dwoma punktami, wzrost, do poziomej zmiany między tymi samymi dwoma punktami, biegiem.

$$ slope = \ frac {rise} {run} = \ frac {change \: in \: y} {change \: in \: x} $$

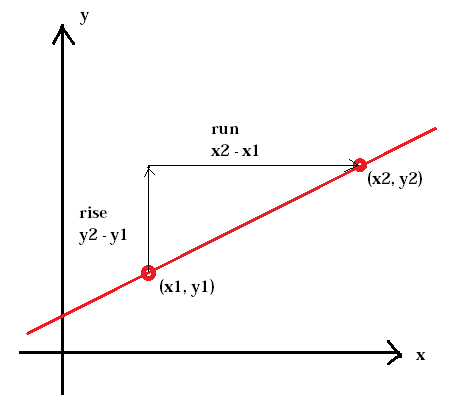
nachylenie linii jest zwykle reprezentowane przez literę m. (x1, y1) reprezentuje pierwszy punkt, podczas gdy (x2, y2) reprezentuje drugi punkt.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Ważne jest, aby zachować tę samą kolejność współrzędnych x i y zarówno w liczniku, jak i w mianowniku, w przeciwnym razie nachylenie będzie nieprawidłowe.

Przykład

Wyznacz nachylenie prostej

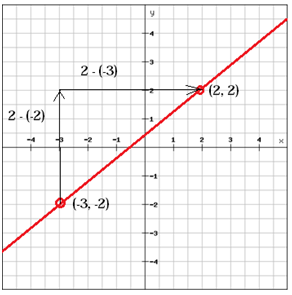
(x1, y1 ) = (-3, -2) i (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

Linia o dodatnim nachyleniu (m > 0), jak linia powyżej, wznosi się od lewej do prawej, natomiast linia o ujemnym nachyleniu (m < 0) opada od lewej do prawej.

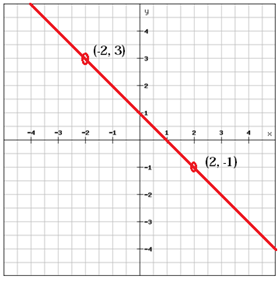
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Jeśli dwie linie mają takie samo nachylenie, mówi się, że są to p arallel.

Możesz wyrazić funkcję liniową za pomocą postaci przecięcia z nachyleniem.

$$ y = mx + b $$

$$ m = slope $ $

$$ b = y – przecięcie $$

Lekcja wideo

Znajdź nachylenie