Obliczenia siły

Siła to pchanie lub ciągnięcie.
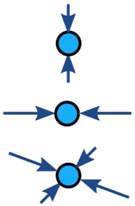
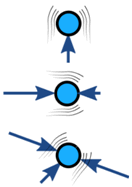
Siły działające na obiekt są zwykle równoważone (jeśli niezrównoważone, obiekt przyspiesza):
 |
 |
|
| Zrównoważony | Niezrównoważony | |
|---|---|---|
| Bez przyspieszenia | Przyspieszenie |
Przykład: siły na szczycie tej wieży mostu są zrównoważone (nie przyspiesza):

Kable ciągną się w dół równo w lewo i w prawo, co jest równoważone przez popychanie wieży do góry. (Czy wieża pcha? Tak! Wyobraź sobie, że stoisz tam zamiast wieży.)
Możemy modelować siły w następujący sposób:

A kiedy ułóż je łeb w ogon, widzimy, że zamykają się z powrotem, co oznacza, że efekt netto wynosi zero:

Siły są w równowadze.
O siłach w równowadze mówi się, że są w równowadze: nie ma też zmian w ruchu.
Diagramy wolnego ciała
Pierwszym krokiem jest do narysowania diagramu swobodnego ciała (zwanego również diagramem sił).
Diagram swobodnego ciała: szkic, w którym ciało zostaje odcięte od świata z wyjątkiem sił działających na nie.
W przykładzie mostu diagram swobodnej bryły górnej części wieży to:

Schemat swobodnego ciała
To pomaga musimy jasno przemyśleć siły działające na ciało.
Przykład: samochód na autostradzie
Jakie siły działają na samochód jadący po autostradzie?

Silnik ciężko pracuje, więc dlaczego samochód nie przyspiesza dalej?
Ponieważ jazda siła jest równoważona przez:
- Opór powietrza (po prostu: gr powietrze nie jest popychane dookoła),
- Opór toczenia, zwany także tarciem tocznym (opony opierają się zmianie kształtu)

Schemat swobodnego nadwozia
W to masa samochodu,
R1 i R2 to opór toczenia opon,
N1 i N2 to siły reakcji (równoważące ciężar samochodu).
Uwaga: koła stalowe (jak w pociągach) mają mniejszy opór toczenia, ale są zbyt śliskie na drodze!
Obliczenia
Siła jest wektorem. Wektor ma wielkość (rozmiar) i kierunek:

Możemy modelować siły, rysując strzałki o odpowiednim rozmiarze i kierunku . W ten sposób:
Przykład: podziwianie widoku
Brady stoi na krawędzi balkonu wspartego na poziomej belce i rozpórce:

Waży 80 kg.
Jakie są siły?
Zajmijmy miejsce, na którym stoi i pomyślmy o siłach, które tam są:

Jego waga
Jego 80-kilogramowa masa wywiera działającą w dół siłę spowodowaną grawitacją.
Siła to masa razy przyspieszenie: F = ma
Przyspieszenie ziemskie spowodowane grawitacją wynosi 9,81 m / s2 więc a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Inne siły
Siły są zbalansowane, więc powinny się zamknąć w ten sposób:

Możemy użyć trygonometrii do rozwiązania tego problemu .
Ponieważ jest to trójkąt prostokątny, SOHCAHTOA pomoże.
W przypadku wiązki znamy sąsiadujący, chcemy znać przeciwieństwo, a „TOA” mówi nam, aby używać stycznej:
opalenizna (60 ° ) = Belka / 785 N
Belka / 785 N = Tan (60 °)
Belka = tan (60 °) × 785 N
Belka = 1,732 … × 785 N = 1360 N
W przypadku Strut znamy sąsiadujący, chcemy znać przeciwprostokątną, a „CAH” mówi nam, aby używać kosinusa:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Rozwiązany:

Ciekawe, jak duża jest siła belka i rozpórka w porównaniu do obsługiwanego ciężaru!
Moment (lub Moment)
A co, jeśli belka jest po prostu wbita w ścianę (zwana wspornikiem)?

Nie ma podpory, więc co się dzieje z siłami?
Diagram swobodnego ciała wygląda następująco:

Siła działająca w górę R równoważy ciężar w dół.
Tylko z tymi dwoma zmusza promień do obracania się jak śmigło! Ale jest też „efekt skrętu” M zwany Momentem (lub Momentem), który to równoważy:
Moment: Siła razy odległość pod kątem prostym.
Wiemy, że waga to 785 N, a także musimy znać odległość pod kątem prostym, która w tym przypadku wynosi 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
I ten moment to właśnie powstrzymuje obracanie się wiązki.

Możesz poczuć chwilę, trzymając wędkę.
Oprócz utrzymywania ciężaru, musisz powstrzymać jego obracanie się w dół.
Tarcie
Pudełko na rampie
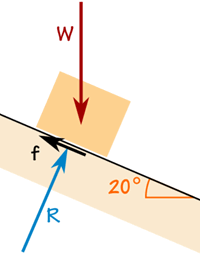
Pudełko waży 100 kg.
Siła tarcia jest wystarczająca, aby utrzymać je tam, gdzie jest.
Siła reakcji R jest prostopadła do rampa.
Skrzynia nie przyspiesza, więc siły są w równowadze:
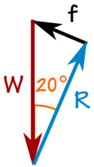
100 Masa kg tworzy siłę działającą w dół ze względu na grawitację:
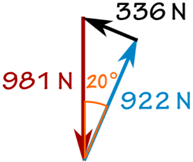
W = 100 kg × 9,81 m / s2 = 981 N
Do rozwiązania trójkąta możemy użyć SOHCAHTOA.
Tarcie f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reakcja N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
I otrzymujemy:
Wskazówki dotyczące rysowania dowolnych diagramów brył
- Rysuj tak prosto, jak to możliwe. Pudełko jest często wystarczające.
- Siły wskazują kierunek, w którym działają na ciało.
- proste strzałki dla sił
- zakrzywione strzałki dla chwil
Sam i Alex wyciągają pudełko
Obliczenia mogą być czasami łatwiejsze, gdy zamienimy wielkość i kierunek na xiy:
 |
< = > |  |
| Wektor a we współrzędnych biegunowych | Wektor a w kartezjańskim współrzędnych |
Możesz przeczytać, jak przekonwertować je na biegunowe i kartezjańskie Współrzędne, ale oto krótkie podsumowanie:
Wykorzystajmy je!