Testy parametryczne i nieparametryczne do porównywania dwóch lub więcej grup

Statystyki: testy parametryczne i nieparametryczne

Ta sekcja obejmuje:

• Wybór testu
• Testy parametryczne
• Testy nieparametryczne

Wybór testu

Jeśli chodzi o wybór testu statystycznego, najważniejszym pytaniem jest „jaka jest główna hipoteza badania?” W niektórych przypadkach nie ma hipotezy; badacz chce po prostu „zobaczyć, co tam jest”. Na przykład w badaniu rozpowszechnienia nie ma żadnej hipotezy do przetestowania, a rozmiar badania zależy od tego, jak dokładnie badacz chce określić chorobowość. Jeśli nie ma hipotezy, nie ma testu statystycznego. Ważne jest, aby zdecydować a priori, które hipotezy są potwierdzające (to znaczy testują pewną z góry założoną zależność), a które są eksploracyjne (sugerują dane). Żadne pojedyncze badanie nie może poprzeć całej serii hipotez. Rozsądnym planem jest poważne ograniczenie liczby hipotez potwierdzających. Chociaż zasadne jest stosowanie testów statystycznych na hipotezach sugerowanych przez dane, wartości P należy traktować jedynie jako wytyczne, a wyniki traktować jako orientacyjne do czasu potwierdzenia w kolejnych badaniach. Przydatnym przewodnikiem jest użycie poprawki Bonferroniego, która stwierdza po prostu, że testując n niezależnych hipotez, należy użyć poziomu istotności 0,05 / n. Zatem gdyby istniały dwie niezależne hipotezy, wynik zostałby uznany za istotny tylko wtedy, gdyby P < 0,025. Należy zauważyć, że ponieważ testy rzadko są niezależne, jest to procedura bardzo konserwatywna – tj. Taka, która prawdopodobnie nie odrzuci hipotezy zerowej. Badacz powinien następnie zapytać „czy dane są niezależne?” Może to być trudne do podjęcia, ale z reguły wyniki dotyczące tej samej osoby lub dopasowanych osób nie są niezależne. Zatem wyniki z próby krzyżowej lub z badania kliniczno-kontrolnego, w którym kontrole zostały dopasowane do przypadków według wieku, płci i klasy społecznej, nie są niezależne.

• Analiza powinna odzwierciedlać projekt , dlatego po dopasowanym projekcie powinna nastąpić analiza dopasowana.
• Wyniki mierzone w czasie wymagają szczególnej uwagi. Jednym z najczęstszych błędów w analizie statystycznej jest traktowanie skorelowanych zmiennych tak, jakby były niezależne. Na przykład, przypuśćmy, że przyglądamy się leczeniu owrzodzeń nóg, w których niektórzy ludzie mieli owrzodzenia na każdej nodze. Możemy mieć 20 badanych z
  30 owrzodzeniami, ale liczba niezależnych informacji wynosi 20, ponieważ stan owrzodzeń na każdej nodze u jednej osoby może zależeć od stanu zdrowia tej osoby i analizy, która uważać wrzody za niezależne obserwacje byłyby błędne. W celu prawidłowej analizy mieszanych sparowanych i niesparowanych
  danych należy skonsultować się ze statystykiem.

Następne pytanie brzmi „jakie typy danych są mierzone?” Zastosowany test powinien być określony na podstawie danych. Wybór testu dla danych dopasowanych lub sparowanych opisano w Tabeli 1, a dla danych niezależnych w Tabeli 2.

Tabela 1 Wybór testu statystycznego na podstawie sparowanej lub dopasowanej obserwacji

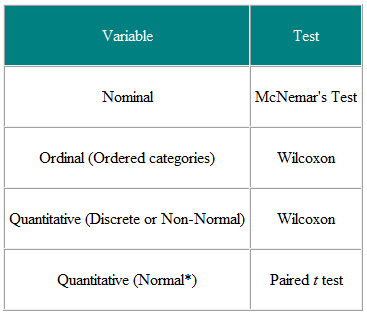
Przydatne jest określenie zmiennych wejściowych i zmiennych wynikowych. Na przykład w badaniu klinicznym zmienną wejściową jest rodzaj leczenia – zmienna nominalna – a wynikiem może być pewna miara kliniczna, być może o rozkładzie normalnym. Wymaganym testem jest więc test t (tabela 2). Jeśli jednak zmienna wejściowa jest ciągła, powiedzmy wynik kliniczny, a wynik jest nominalny, powiedzmy wyleczony lub nie wyleczony, wymagana jest analiza regresji logistycznej. Test t w tym przypadku może pomóc, ale nie dałby nam tego, czego wymagamy, a mianowicie prawdopodobieństwa wyleczenia przy danej wartości wyniku klinicznego. Jako inny przykład załóżmy, że mamy badanie przekrojowe, w którym pytamy losowo wybraną grupę osób, czy uważają, że ich lekarz pierwszego kontaktu wykonuje dobrą pracę, na pięciostopniowej skali, i chcielibyśmy ustalić, czy kobiety mają wyższą opinię lekarzy ogólnych niż mężczyźni. Zmienną wejściową jest płeć, która jest nominalna. Zmienną wyniku jest pięciostopniowa skala porządkowa. Opinia każdej osoby jest niezależna od innych, więc mamy niezależne dane. Z tabeli 2 powinniśmy użyć testu χ2 dla trendu lub testu U Manna-Whitneya z poprawką na remisy (uwaga: remis występuje, gdy dwa lub więcej wartości są takie same, więc nie ma ściśle rosnącego porządku rang – w takim przypadku można uśrednić rangi dla wartości powiązanych) .Należy jednak pamiętać, że jeśli jedni dzielą lekarza rodzinnego, a inni nie, to dane nie są wymagana jest niezależna i bardziej wyrafinowana analiza. Należy pamiętać, że tabele te należy traktować jedynie jako wskazówki, a każdy przypadek należy rozpatrywać pod względem merytorycznym.

Tabela 2 Wybór testu statystycznego dla niezależnych obserwacji

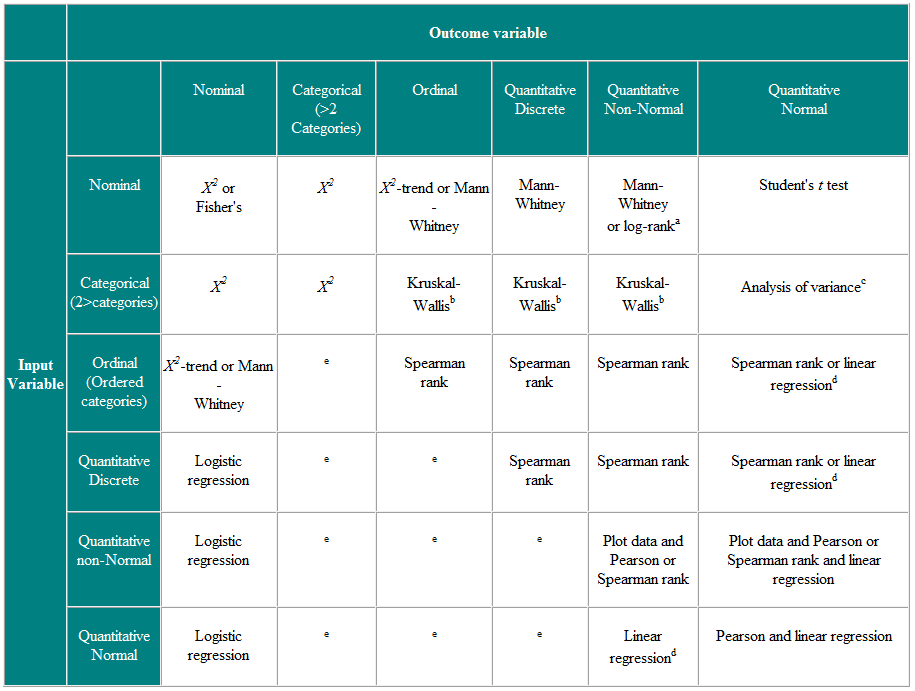
a Jeśli dane są cenzurowane. b Test Kruskala-Wallisa służy do porównywania zmiennych porządkowych lub zmiennych innych niż normalne dla więcej niż dwóch grup i jest uogólnieniem testu U Manna-Whitneya. c Analiza wariancji jest techniką ogólną, a jedna wersja (jednokierunkowa analiza wariancji) jest używana do porównywania zmiennych o rozkładzie normalnym dla więcej niż dwóch grup i jest parametrycznym odpowiednikiem Kruskala-Wallistestu. d Jeśli zmienna wynikowa jest zmienną zależną, to pod warunkiem, że reszty (różnice między obserwowanymi wartościami a przewidywanymi odpowiedziami z regresji) mają prawdopodobny rozkład normalny, wówczas rozkład zmiennej niezależnej nie jest ważny. e Istnieje wiele bardziej zaawansowanych technik, takich jak regresja Poissona, służących do radzenia sobie w takich sytuacjach. Wymagają jednak pewnych założeń i często łatwiej jest albo dychotomizować zmienną wynikową, albo traktować ją jako ciągłą.

Testy parametryczne to te, które przyjmują założenia dotyczące parametrów rozkładu populacji, z którego pobierana jest próbka . Jest to często założenie, że dane dotyczące populacji mają rozkład normalny. Testy nieparametryczne są „wolne od dystrybucji” i jako takie mogą być stosowane dla zmiennych innych niż normalne. Tabela 3 przedstawia nieparametryczny odpowiednik szeregu testów parametrycznych.

Tabela 3 Parametryczne i Testy nieparametryczne do porównywania dwóch lub więcej grup

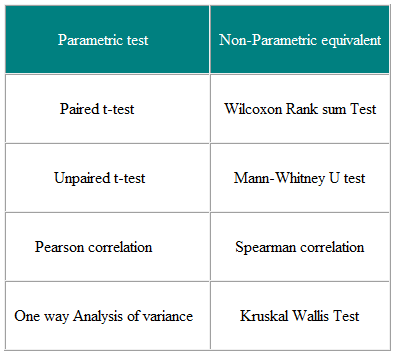
Testy nieparametryczne są ważne zarówno dla danych o rozkładzie nienormalnym, jak i Dane rozproszone normalnie, więc dlaczego nie używać ich cały czas?

We wszystkich przypadkach rozsądne byłoby stosowanie testów nieparametrycznych, co pozwoliłoby zaoszczędzić kłopotów z testowaniem pod kątem normalności. Preferowane są testy parametryczne, jednakże z następujących powodów:

1. Rzadko jesteśmy zainteresowani samym testem istotności; chcielibyśmy coś powiedzieć o populacji, z której pochodzą próbki, a najlepiej to zrobić za pomocą
oszacowania parametrów i przedziałów ufności.

2. Trudno jest przeprowadzić elastyczne modelowanie za pomocą testów nieparametrycznych, na przykład dopuszczając czynniki zakłócające przy użyciu wielu regresja.

3. Testy parametryczne mają zwykle większą moc statystyczną niż ich nieparametryczne odpowiedniki. Innymi słowy, istnieje większe prawdopodobieństwo wykrycia znaczących różnic, gdy
one naprawdę istnieją.

Czy testy nieparametryczne porównują mediany?

Powszechnie uważa się, że Test U Manna-Whitneya jest w rzeczywistości testem na różnice w medianach. Jednak dwie grupy mogą mieć tę samą medianę, a mimo to mieć znaczący test U Manna-Whitneya. Rozważ następujące dane dla dwóch grup, z których każda zawiera 100 obserwacji. Grupa 1: 98 (0), 1, 2; Grupa 2:51 (0), 1, 48 (2). Mediana w obu przypadkach wynosi 0, ale z testu Manna-Whitneya P < 0,0001. Tylko jeśli jesteśmy gotowi przyjąć dodatkowe założenie, że różnica w obu grupach jest po prostu zmianą lokalizacji (to znaczy, że dystrybucja danych w jednej grupie jest po prostu przesunięta o ustaloną wartość w stosunku do drugiej), możemy powiedzieć, że test jest testem różnicy median. Jeśli jednak grupy mają ten sam rozkład, to zmiana położenia spowoduje przesunięcie median i średnich o tę samą wartość, a zatem różnica w medianach jest taka sama, jak różnica średnich. Zatem test U Manna-Whitneya jest również testem różnicy średnich. Jaki jest związek testu U Manna-Whitneya z testem t-Studenta? Gdyby wprowadzić szeregi danych, a nie same dane, do programu testu t dla dwóch próbek, otrzymana wartość P byłaby bardzo zbliżona do uzyskanej w teście U Manna-Whitneya.