• K-vizinho mais próximo é um dos mais simples algoritmos de aprendizado de máquina na técnica de Aprendizagem Supervisionada.
• O algoritmo K-NN assume a similaridade entre o novo caso / dados e os casos disponíveis e coloca o novo caso na categoria que é mais semelhante às categorias disponíveis.

K-NN armazena todos os dados disponíveis e classifica um novo ponto de dados com base na similaridade. Isso significa que quando novos dados aparecem, eles podem ser facilmente classificados em uma categoria de suíte usando o algoritmo K-NN.

• O algoritmo K-NN pode ser usado para regressão, bem como para classificação, mas principalmente é usado para os problemas de classificação.
• K-NN é um algoritmo não paramétrico, o que significa ele não faz nenhuma suposição sobre os dados subjacentes.
• Também é chamado de algoritmo de aprendizado preguiçoso porque não aprende com o conjunto de treinamento imediatamente, em vez de armazenar o conjunto de dados e, no momento da classificação, realiza um ação no conjunto de dados.
• O algoritmo KNN na fase de treinamento apenas armazena o conjunto de dados e, quando obtém novos dados, classifica esses dados em uma categoria muito semelhante aos novos dados.
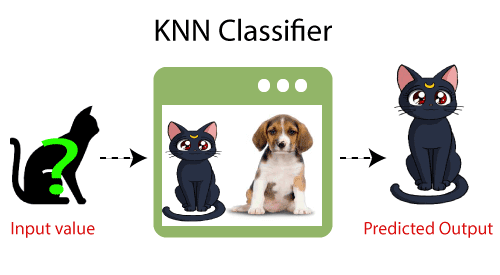
• Exemplo: suponha que temos a imagem de uma criatura que se parece com um gato e um cachorro, mas queremos saber se é um gato ou um cachorro. Então, para essa identificação, podemos usar o algoritmo KNN, pois ele trabalha em uma medida de similaridade. Nosso modelo KNN encontrará os recursos semelhantes do novo conjunto de dados para as imagens de cães e gatos e, com base nos recursos mais semelhantes, ele o colocará na categoria de gato ou cachorro.

Por que precisamos de um algoritmo K-NN?

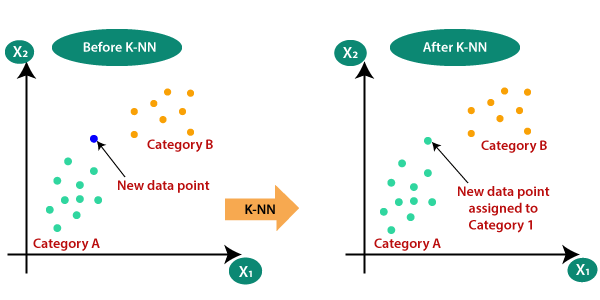
Suponha que haja duas categorias, ou seja, Categoria A e Categoria B, e temos um novo ponto de dados x1, portanto, esse ponto de dados estará em qual dessas categorias. Para resolver esse tipo de problema, precisamos de um algoritmo K-NN. Com a ajuda de K-NN, podemos identificar facilmente a categoria ou classe de um determinado conjunto de dados. Considere o diagrama abaixo:

Como funciona o K-NN?

O funcionamento do K-NN pode ser explicado com base em o algoritmo abaixo:

• Etapa 1: Selecione o número K de vizinhos
• Etapa 2: Calcule a distância euclidiana de K número de vizinhos
• Etapa 3: tome os K vizinhos mais próximos de acordo com a distância euclidiana calculada.
• Etapa 4: Entre esses k vizinhos, conte o número de pontos de dados em cada categoria.
• Etapa 5: atribua os novos pontos de dados à categoria para a qual o número do vizinho é máximo.
• Etapa 6: Nosso modelo está pronto.

Suponha que temos um novo ponto de dados e precisamos colocá-lo na categoria necessária. Considere a imagem abaixo:

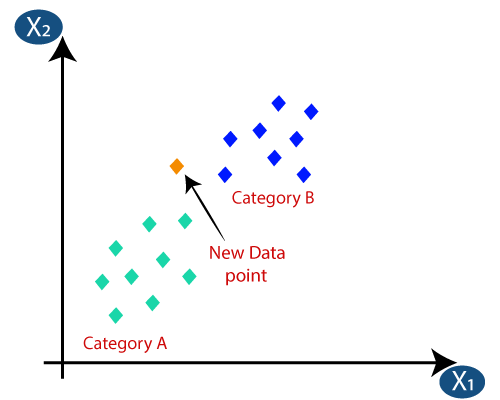
• Primeiramente, escolheremos o número de vizinhos, portanto, escolheremos k = 5.
• A seguir, calcularemos a distância euclidiana entre os pontos de dados. A distância euclidiana é a distância entre dois pontos, que já estudamos em geometria. Pode ser calculado como:

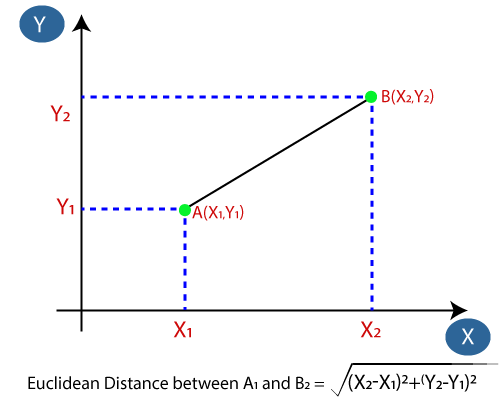
• Calculando a distância euclidiana, obtivemos os vizinhos mais próximos, como três vizinhos mais próximos na categoria A e dois vizinhos mais próximos na categoria B. Considere a imagem abaixo:

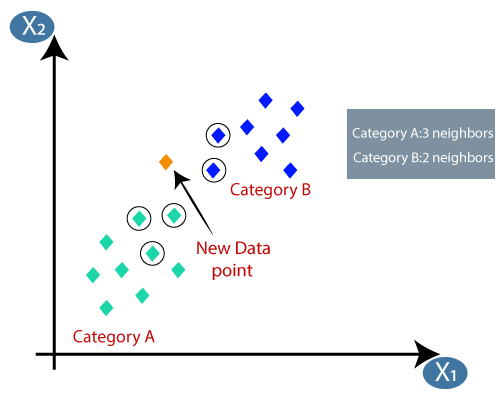
• Como podemos ver, os 3 vizinhos mais próximos são da categoria A, portanto, este novo ponto de dados deve pertencer à categoria A.

Como selecionar o valor de K no algoritmo K-NN?

Abaixo estão alguns pontos para lembre-se ao selecionar o valor de K no algoritmo K-NN:

• Não há uma maneira particular de determinar o melhor valor para “K”, então precisamos tentar alguns valores para encontrar o melhor fora deles. O valor mais preferido para K é 5.
• Um valor muito baixo para K, como K = 1 ou K = 2, pode ser ruidoso e levar aos efeitos de outliers no modelo.
• Valores grandes para K são bons, mas podem encontrar algumas dificuldades.

Vantagens do algoritmo KNN:

• É simples de implementar.
• É robusto para dados de treinamento ruidosos
• Pode ser mais eficaz se os dados de treinamento forem grandes.

Desvantagens do algoritmo KNN:

• Sempre precisa determinar o valor de K que pode ser complexo em algum momento.
• O custo de computação é alto por causa do cálculo da distância entre os pontos de dados para todas as amostras de treinamento .

Implementação Python do algoritmo KNN

Para fazer a implementação Python do algoritmo K-NN, usaremos o mesmo problema e conjunto de dados que usamos em Regressão Logística. Mas aqui vamos melhorar o desempenho do modelo. Abaixo está a descrição do problema:

Problema para o algoritmo K-NN: Há um fabricante de automóveis que fabricou um carro SUV novo.A empresa deseja fornecer os anúncios aos usuários interessados em comprar aquele SUV. Portanto, para este problema, temos um conjunto de dados que contém informações de vários usuários por meio da rede social. O conjunto de dados contém muitas informações, mas o salário estimado e a idade consideraremos para a variável independente e a variável comprada é para a variável dependente. Abaixo está o conjunto de dados:

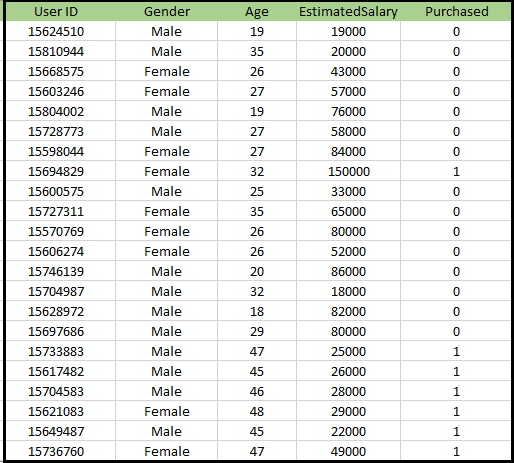
Etapas para implementar o algoritmo K-NN:

• Etapa de pré-processamento de dados
• Ajustando o algoritmo K-NN ao conjunto de treinamento
• Previsão do resultado do teste
• Precisão do teste do resultado (Criação da matriz de confusão)
• Visualizando o resultado do conjunto de teste.

Etapa de pré-processamento de dados:

A etapa de pré-processamento de dados permanecerá exatamente igual à regressão logística. Abaixo está o código para isso:

Ao executar o código acima, nosso conjunto de dados é importado para nosso programa e bem pré-processado. Após o dimensionamento de recursos, nosso conjunto de dados de teste ficará assim:

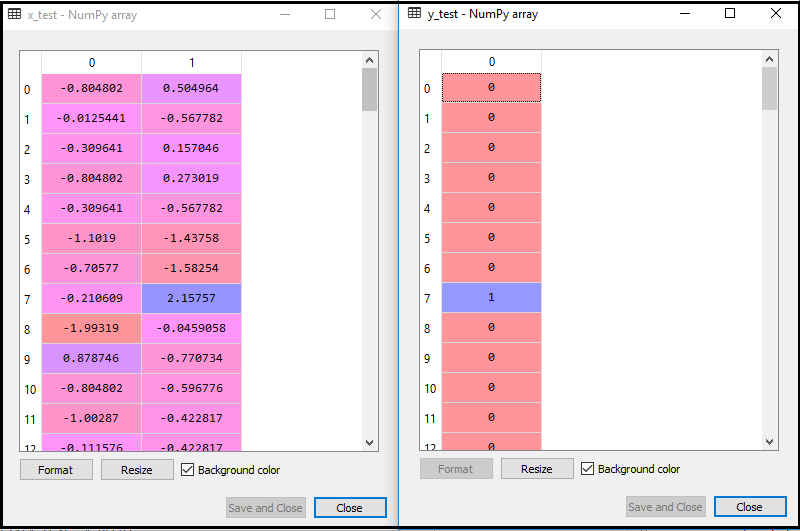
Do resultado acima im idade, podemos ver que nossos dados foram dimensionados com sucesso.

• Ajustando o classificador K-NN aos dados de treinamento:
  Agora, ajustaremos o classificador K-NN aos dados de treinamento. Para fazer isso, importaremos a classe KNeighborsClassifier da biblioteca Sklearn Neighbours. Após importar a classe, iremos criar o objeto Classifier da classe. O parâmetro desta classe será
  • n_neighbors: Para definir os vizinhos necessários do algoritmo. Normalmente leva 5.
  • metric = “minkowski”: Este é o parâmetro padrão e ele decide a distância entre os pontos.
  • p = 2: É equivalente ao padrão Métrica euclidiana.

  E então ajustaremos o classificador aos dados de treinamento. Abaixo está o código para isso:

Resultado: Ao executar o código acima, obteremos o resultado como:

• Previsão do resultado do teste: Para prever o resultado do conjunto de teste, criaremos um vetor y_pred como fizemos na regressão logística. Abaixo está o código para ele:

Saída:

A saída para o código acima será:

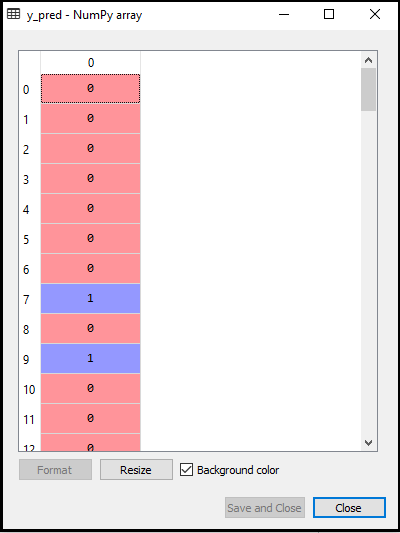
• Criando a matriz de confusão:
  Agora vamos criar a Matriz de confusão para nosso modelo K-NN para ver a precisão do classificador. Abaixo está o código para isso:

No código acima, importamos a função confusão_matrix e a chamamos usando a variável cm.

Resultado: Ao executar o código acima, obteremos a matriz conforme abaixo:

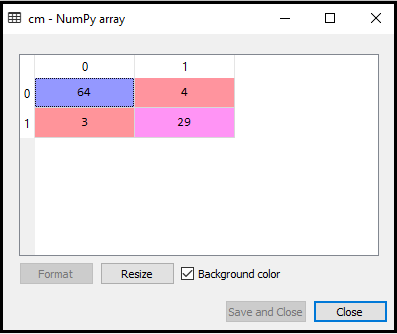
Na imagem acima, podemos ver existem 64 + 29 = 93 previsões corretas e 3 + 4 = 7 previsões incorretas, enquanto que, na Regressão Logística, houve 11 previsões incorretas. Portanto, podemos dizer que o desempenho do modelo é melhorado usando o algoritmo K-NN.

• Visualizando o resultado do conjunto de treinamento:
  Agora, vamos visualizar o resultado do conjunto de treinamento para K Modelo -NN. O código permanecerá o mesmo que fizemos na Regressão Logística, exceto o nome do gráfico. Abaixo está o código para ele:

Resultado:

Ao executar o código acima, obteremos o gráfico abaixo:

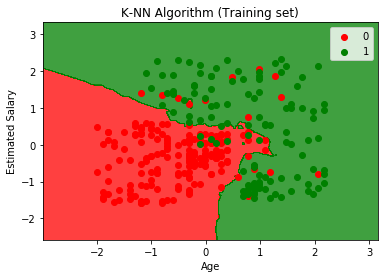
O gráfico de saída é diferente do gráfico que ocorremos na Regressão Logística. Pode ser entendido nos pontos abaixo:

• Como podemos ver o gráfico está mostrando o ponto vermelho e os pontos verdes. Os pontos verdes são para a variável Comprado (1) e Pontos vermelhos para a variável não comprado (0).
• O gráfico está mostrando um limite irregular em vez de mostrar qualquer linha reta ou qualquer curva porque é um algoritmo K-NN, ou seja, encontrando o vizinho mais próximo.
• O gráfico classificou os usuários nas categorias corretas, já que a maioria dos usuários que não compraram o SUV está na região vermelha e os usuários que compraram o SUV estão na região verde.
• O gráfico está mostrando um bom resultado, mas ainda existem alguns pontos verdes na região vermelha e pontos vermelhos na região verde. Mas isso não é um grande problema, pois ao fazer este modelo evita-se problemas de sobreajuste.
• Portanto, nosso modelo é bem treinado.
• Visualizando o resultado do conjunto de teste:
  Após o treinamento do modelo, iremos agora testar o resultado colocando um novo conjunto de dados, ou seja, Conjunto de dados de teste. O código permanece o mesmo, exceto algumas pequenas alterações: como x_train e y_train serão substituídos por x_test e y_test.
  Abaixo está o código para ele:

Resultado:

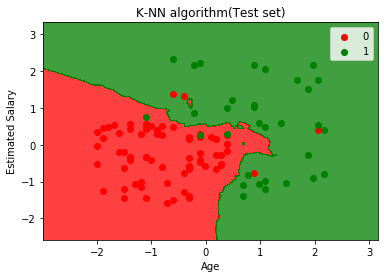
O gráfico acima mostra a saída para o conjunto de dados de teste. Como podemos ver no gráfico, a saída prevista é boa bom, pois a maioria dos pontos vermelhos estão na região vermelha e a maioria dos pontos verdes está na região verde.

No entanto, existem alguns pontos verdes na região vermelha e alguns pontos vermelhos na região verde. Portanto, essas são as observações incorretas que observamos na matriz de confusão (7 saída incorreta).