Testes paramétricos e não paramétricos para comparar dois ou mais grupos

Estatística: testes paramétricos e não paramétricos

Esta seção abrange:

• Escolha de um teste
• Testes paramétricos
• Testes não paramétricos

Escolha de um teste

Em termos de seleção de um teste estatístico, a questão mais importante é “qual é a hipótese principal do estudo?” Em alguns casos, não há hipótese; o investigador só quer “ver o que está lá”. Por exemplo, em um estudo de prevalência, não há hipótese para testar, e o tamanho do estudo é determinado pela precisão com que o investigador deseja determinar a prevalência. Se não houver hipótese, não há teste estatístico. É importante decidir a priori quais hipóteses são confirmatórias (isto é, estão testando alguma relação pressuposta) e quais são exploratórias (são sugeridas pelos dados). Nenhum estudo pode apoiar toda uma série de hipóteses. Um plano sensato é limitar severamente o número de hipóteses confirmatórias. Embora seja válido o uso de testes estatísticos nas hipóteses sugeridas pelos dados, os valores de P devem ser usados apenas como orientação, e os resultados tratados como tentativas até confirmados por estudos subsequentes. Um guia útil é usar uma correção de Bonferroni, que afirma simplesmente que se alguém está testando n hipóteses independentes, deve-se usar um nível de significância de 0,05 / n. Assim, se houvesse duas hipóteses independentes, um resultado seria declarado significativo apenas se P < 0,025. Observe que, uma vez que os testes raramente são independentes, este é um procedimento muito conservador – ou seja, é improvável que rejeite a hipótese nula. O investigador deve então perguntar “os dados são independentes?” Isso pode ser difícil de decidir, mas, como regra geral, os resultados no mesmo indivíduo, ou de indivíduos compatíveis, não são independentes. Assim, os resultados de um ensaio cruzado ou de um estudo de caso-controle em que os controles foram pareados aos casos por idade, sexo e classe social não são independentes.

• A análise deve refletir o desenho e, portanto, um design compatível deve ser seguido por uma análise compatível.
• Os resultados medidos ao longo do tempo requerem cuidado especial. Um dos erros mais comuns na análise estatística é tratar as variáveis correlacionadas como se fossem independentes. Por exemplo, suponha que estejamos olhando para o tratamento de úlceras de perna, em que algumas pessoas tinham uma úlcera em cada perna. Podemos ter 20 indivíduos com
  30 úlceras, mas o número de peças independentes de informação é 20 porque o estado das úlceras em cada perna de uma pessoa pode ser influenciado pelo estado de saúde da pessoa e uma análise de que considerar úlceras como observações independentes seriam incorretas. Para uma análise correta de dados mistos emparelhados e não emparelhados, consulte um estatístico.

A próxima pergunta é “que tipos de dados estão sendo medidos?” O teste usado deve ser determinado pelos dados. A escolha do teste para dados combinados ou emparelhados é descrita na Tabela 1 e para dados independentes na Tabela 2.

Tabela 1 Escolha do teste estatístico a partir de observação emparelhada ou combinada

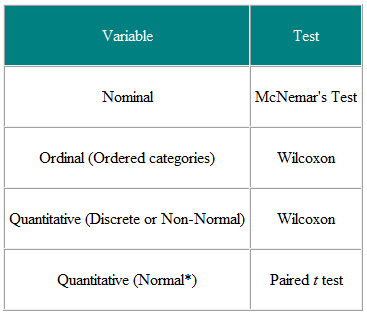
É útil decidir as variáveis de entrada e as variáveis de resultado. Por exemplo, em um ensaio clínico, a variável de entrada é o tipo de tratamento – uma variável nominal – e o resultado pode ser alguma medida clínica, talvez normalmente distribuída. O teste necessário é então o teste t (Tabela 2). No entanto, se a variável de entrada for contínua, digamos um escore clínico, e o resultado for nominal, digamos curado ou não curado, a regressão logística é a análise necessária. Um teste t, neste caso, pode ajudar, mas não nos daria o que exigimos, ou seja, a probabilidade de cura para um determinado valor do escore clínico. Como outro exemplo, suponha que temos um estudo transversal no qual perguntamos a uma amostra aleatória de pessoas se elas acham que seu clínico geral está fazendo um bom trabalho, em uma escala de cinco pontos, e desejamos verificar se as mulheres têm uma opinião mais elevada de clínicos gerais do que os homens. A variável de entrada é gênero, que é nominal. A variável de resultado é a escala ordinal de cinco pontos. A opinião de cada pessoa é independente das outras, portanto, temos dados independentes. A partir da Tabela 2, devemos usar um teste χ2 para tendência, ou um teste U de Mann-Whitney com uma correção para empates (NB ocorre um empate onde dois ou mais os valores são iguais, portanto, não há ordem estritamente crescente de classificações – onde isso acontece, pode-se calcular a média das classificações para valores empatados. Observe, no entanto, se algumas pessoas compartilham um clínico geral e outras não, os dados não são É necessária uma análise independente e mais sofisticada Observe que essas tabelas devem ser consideradas apenas como guias, e cada caso deve ser considerado de acordo com seus méritos.

Tabela 2 Escolha do teste estatístico para observações independentes

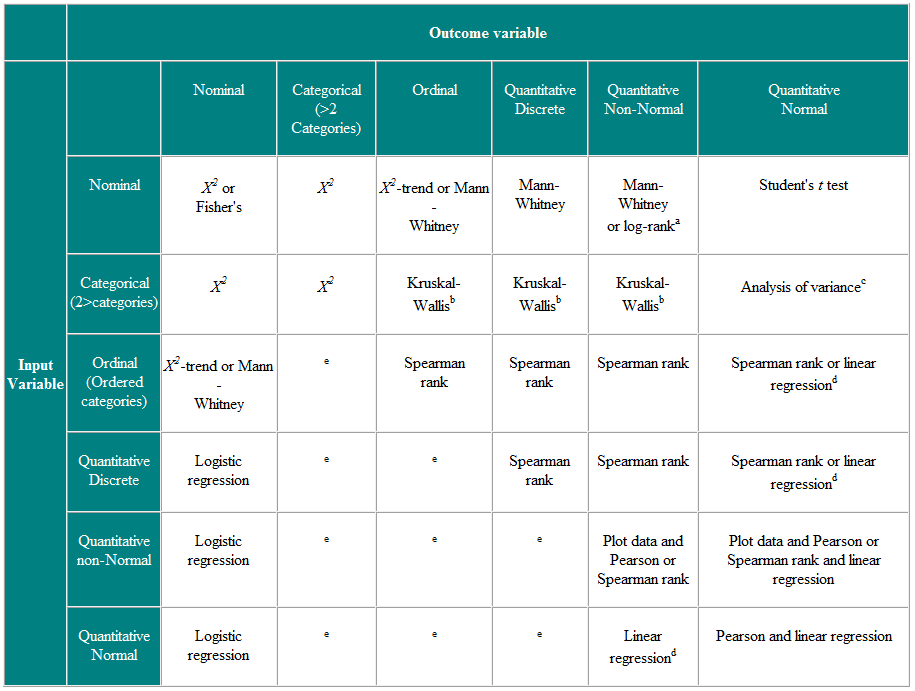
a Se os dados forem censurados. b O teste de Kruskal-Wallis é usado para comparar variáveis ordinais ou não normais para mais de dois grupos e é uma generalização do teste U de Mann-Whitney. c A análise de variância é uma técnica geral, e uma versão (análise de variância unilateral) é usada para comparar variáveis normalmente distribuídas para mais de dois grupos e é o equivalente paramétrico do Kruskal-Wallistest. d Se a variável de resultado for a variável dependente, então, desde que os resíduos (as diferenças entre os valores observados e as respostas previstas da regressão) sejam plausivelmente distribuídas normalmente, então a distribuição da variável independente não é importante. e Existem várias técnicas mais avançadas, como a regressão de Poisson, para lidar com essas situações. No entanto, eles exigem certas suposições e muitas vezes é mais fácil dicotomizar a variável de resultado ou tratá-la como contínua.

Os testes paramétricos são aqueles que fazem suposições sobre os parâmetros da distribuição da população da qual a amostra é retirada . Freqüentemente, pressupõe-se que os dados populacionais são normalmente distribuídos. Os testes não paramétricos são “livres de distribuição” e, como tal, podem ser usados para variáveis não normais. A Tabela 3 mostra o equivalente não paramétrico de uma série de testes paramétricos.

Tabela 3 Paramétricos e Testes não paramétricos para comparar dois ou mais grupos

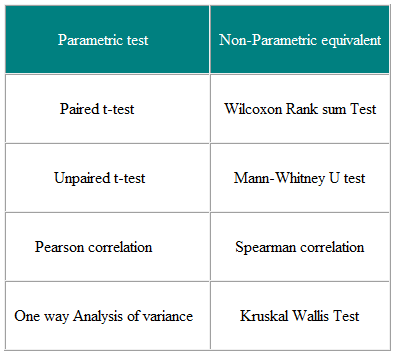
Testes não paramétricos são válidos para dados não normalmente distribuídos e Dados normalmente distribuídos, então por que não usá-los o tempo todo?

Parece prudente usar testes não paramétricos em todos os casos, o que evitaria o incômodo de testar a normalidade. Os testes paramétricos são preferidos, no entanto, pelos seguintes motivos:

1. Raramente estamos interessados em um teste de significância sozinho; gostaríamos de dizer algo sobre a população de onde vieram as amostras, e isso é melhor feito com
estimativas de parâmetros e intervalos de confiança.

2. É difícil fazer modelagem flexível com testes não paramétricos, por exemplo, permitindo fatores de confusão usando múltiplos regressão.

3. Os testes paramétricos geralmente têm mais poder estatístico do que seus equivalentes não paramétricos. Em outras palavras, é mais provável detectar diferenças significativas quando
elas realmente existem.

Os testes não paramétricos comparam medianas?

É uma crença comum que um O teste U de Mann-Whitney é, na verdade, um teste para diferenças nas medianas. No entanto, dois grupos podem ter a mesma mediana e ainda assim ter um teste U de Mann-Whitney significativo. Considere os seguintes dados para dois grupos, cada um com 100 observações. Grupo 1: 98 (0), 1, 2; Grupo 2: 51 (0), 1, 48 (2). A mediana em ambos os casos é 0, mas do teste de Mann-Whitney P < 0,0001. Somente se estivermos preparados para fazer a suposição adicional de que a diferença nos dois grupos é simplesmente uma mudança na localização (ou seja, a distribuição dos dados em um grupo é simplesmente deslocada por um valor fixo do outro), podemos dizer que o teste é um teste da diferença de medianas. No entanto, se os grupos tiverem a mesma distribuição, então uma mudança na localização moverá as medianas e as médias na mesma quantidade e, portanto, a diferença nas medianas é igual à diferença nas médias. Assim, o teste U de Mann-Whitney também é um teste para a diferença de médias. Como o teste U de Mann-Whitney está relacionado ao teste t? Se fosse para inserir as classificações dos dados em vez dos próprios dados em um programa de teste t de duas amostras, o valor P obtido seria muito próximo ao produzido por um teste U de Mann-Whitney.