Forçar cálculos

Força é push ou pull.
As forças em um objeto são geralmente equilibradas (se desequilibrado, o objeto acelera):
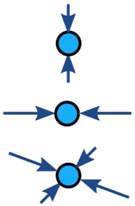 |
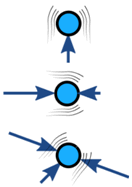 |
|
| Equilibrado | Desequilibrado | |
|---|---|---|
| Sem aceleração | Aceleração |
Exemplo: As forças no topo desta torre da ponte estão em equilíbrio (não está acelerando):

Os cabos puxam para baixo igualmente para a esquerda e para a direita, e isso é equilibrado pela pressão para cima da torre. (A torre empurra? Sim! Imagine que você está lá em vez da torre.)
Podemos modelar as forças assim:

E quando nós coloque-os frente a frente, vemos que eles se fecham, o que significa que o efeito líquido é zero:

As forças estão em equilíbrio.
Diz-se que as forças em equilíbrio estão em equilíbrio: também não há mudança no movimento.
Diagramas de corpo livre
O primeiro passo é para desenhar um Diagrama de corpo livre (também chamado de diagrama de força)
Diagrama de corpo livre: um esboço em que um corpo é separado do mundo, exceto pelas forças que atuam sobre ele.
No exemplo da ponte, o diagrama de corpo livre para o topo da torre é:

Diagrama de corpo livre
Isso ajuda que pensemos claramente sobre as forças que atuam no corpo.
Exemplo: Carro em uma rodovia
Quais são as forças em um carro cruzando a rodovia?

O motor está funcionando muito, então por que o carro não continua a acelerar?
Porque a direção a força é equilibrada por:
- Resistência do ar (simplificando: th O ar resiste a ser empurrado),
- Resistência ao rolamento, também chamada de atrito de rolamento (os pneus resistem a ter sua forma alterada)

Diagrama de corpo livre
W é o peso do carro,
R1 e R2 são a resistência ao rolamento dos pneus,
N1 e N2 são as forças de reação (equilibrando o peso do carro).
Observação: rodas de aço (como em trens) têm menos resistência ao rolamento, mas são muito escorregadias na estrada!
Cálculos
Força é um vetor. Um vetor tem magnitude (tamanho) e direção:

Podemos modelar as forças desenhando setas de tamanho e direção corretos . Assim:
Exemplo: Admirando a vista
Brady está na beira de uma varanda apoiado por uma viga horizontal e um suporte:

Ele pesa 80 kg.
Quais são as forças?
Vamos pegar o lugar em que ele está e pensar sobre as forças ali:

Seu peso
Sua massa de 80 kg cria uma força para baixo devido à gravidade.
Força é a massa vezes a aceleração: F = ma
A aceleração da gravidade na Terra é de 9,81 m / s2 , então a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
As outras forças
As forças estão equilibradas, então elas devem se fechar assim:

Podemos usar trigonometria para resolver isso .
Por ser um triângulo retângulo, SOHCAHTOA ajudará.
Para o Feixe, conhecemos o Adjacente, queremos saber o Oposto, e “TOA” nos diz para usar a Tangente:
bronzeado (60 ° ) = Feixe / 785 N
Feixe / 785 N = tan (60 °)
Feixe = tan (60 °) × 785 N
Feixe = 1,732 … × 785 N = 1360 N
Para o Strut, conhecemos o Adjacente, queremos saber a Hipotenusa e “CAH” nos diz para usar cosseno:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Resolvido:

Interessante a quantidade de força aplicada a viga e o suporte em comparação com o peso que está sendo suportado!
Torque (ou momento)
E se a viga for apenas presa na parede (chamada de cantilever)?

Não há nenhum suporte de apoio, então o que acontece com as forças?
O diagrama de corpo livre é semelhante a:

A força para cima R equilibra o peso para baixo.
Com apenas esses dois força o feixe vai girar como uma hélice! Mas também há um “efeito de rotação” M chamado Momento (ou Torque) que equilibra:
Momento: Força vezes a Distância em ângulos retos.
Sabemos que o Peso é 785 N, e também precisamos saber a distância nos ângulos retos, que neste caso é 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
E aquele momento é o que impede o feixe de girar.

Você pode sentir o momento ao segurar uma vara de pescar.
Além de sustentar seu peso, você precisa impedir que ele gire para baixo.
Fricção
Caixa em uma rampa
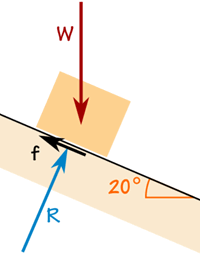
A caixa pesa 100 kg.
A força de atrito é suficiente para mantê-la onde está.
A força de reação R está em ângulo reto com o rampa.
A caixa não está acelerando, então as forças estão equilibradas:
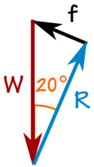
Os 100 kg de massa cria uma força para baixo devido à gravidade:
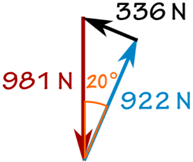
W = 100 kg × 9,81 m / s2 = 981 N
Podemos usar SOHCAHTOA para resolver o triângulo.
Fricção f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reação N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
E obtemos:
Dicas para desenhar diagramas de corpo livre
- Desenhe da forma mais simples possível. Uma caixa costuma ser suficiente.
- As forças apontam na direção em que atuam no corpo
- setas retas para forças
- setas curvas para momentos
Sam e Alex puxam uma caixa
Os cálculos às vezes podem ser mais fáceis quando transformamos magnitude e direção em xey:
 |
< = > |  |
| Vetor a em coordenadas polares | Vetor a em coordenadas cartesianas |
Você pode ler como convertê-los em polar e cartesiano Coordenadas, mas aqui está um resumo rápido:
Vamos usá-las!