Calcule forță

Forța este push sau pull.
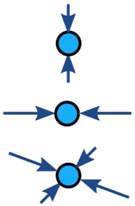
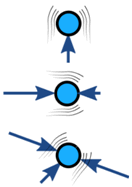
Forțele asupra unui obiect sunt de obicei echilibrate (dacă este dezechilibrat, obiectul accelerează):
 |
 |
|
| Echilibrat | Dezechilibrat | |
|---|---|---|
| Fără accelerare | Accelerare |
Exemplu: Forțele din partea de sus a acestui turn de pod sunt în echilibru (nu accelerează):

Cablurile trag în jos în mod egal la stânga și la dreapta, iar acest lucru este echilibrat de împingerea în sus a turnului. (Împinge turnul? Da! Imaginați-vă că stați acolo în loc de turn.)
Putem modela forțele astfel:

Și când puneți-le cap la coadă, vedem că se închid din nou, ceea ce înseamnă că efectul net este zero:

Forțele sunt în echilibru.
Se spune că forțele în echilibru sunt în echilibru: nu există nici o schimbare în mișcare.
Diagramele corpului liber
Primul pas este pentru a desena o diagramă a corpului liber (numită și diagramă a forței)
Diagrama corpului liber: o schiță în care un corp este tăiat liber de lume, cu excepția forțelor care acționează asupra acestuia.
În exemplul podului, diagrama corpului liber pentru partea de sus a turnului este:

Diagrama corpului liber
Ajută să ne gândim clar la forțele care acționează asupra corpului.
Exemplu: Mașină pe autostradă
Care sunt forțele unei mașini care navighează pe autostradă?

Motorul funcționează din greu, deci de ce mașina nu continuă să accelereze?
Deoarece conducerea forța este echilibrată prin:
- Rezistența la aer (pur și simplu: th Aerul rezistă la împingere),
- Rezistența la rulare, numită și frecare la rulare (anvelopele rezistă la schimbarea formei lor)

Diagrama gratuită a caroseriei
W este greutatea mașinii,
R1 și R2 sunt rezistența la rulare a anvelopelor,
N1 și N2 sunt forțele de reacție (echilibrând greutatea mașinii).
Notă: roțile din oțel (ca la trenuri) au o rezistență la rulare mai mică, dar sunt mult prea alunecoase pe drum!
Calcule
Forța este un vector. Un vector are magnitudine (dimensiune) și direcție:

Putem modela forțele trasând săgeți de dimensiunea și direcția corectă . Așa:
Exemplu: Admirarea priveliștii
Brady stă pe marginea unui balcon susținut de o grindă orizontală și de un suport:

El cântărește 80 kg.
Care sunt forțele?
Să luăm locul pe care stă și să ne gândim la forțele de acolo:

Greutatea Sa
Masa sa de 80 kg creează o forță descendentă datorită gravitației.
Forța este masă ori accelerarea: F = ma
Accelerația datorată gravitației pe Pământ este de 9,81 m / s2 , deci a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
Celelalte Forțe
Forțele sunt echilibrate, așa că ar trebui să se închidă asupra lor astfel:

Putem utiliza trigonometria pentru a o rezolva .
Deoarece este un triunghi unghiular, SOHCAHTOA va ajuta.
Pentru Beam, cunoaștem Adiacentul, vrem să aflăm Opusul și „TOA” ne spune să folosim Tangent:
bronz (60 ° ) = Beam / 785 N
Beam / 785 N = tan (60 °)
Beam = tan (60 °) × 785 N
Beam = 1.732 … × 785 N = 1360 N
Pentru Strut, cunoaștem Adiacentul, vrem să cunoaștem Hipotenuza și „CAH” ne spune să folosim Cosinusul:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0,5 = 1570 N
Rezolvat:

Interesant cât de multă forță este grinda și tija în comparație cu greutatea suportată!
Cuplul (sau momentul)
Ce se întâmplă dacă grinda este doar lipită în perete (numită consolă)?

Nu există un suport de sprijin, deci ce se întâmplă cu forțele?
Diagrama corpului liber arată astfel:

Forța ascendentă R echilibrează greutatea descendentă.
Cu doar cele două forțează fasciculul să se rotească ca o elice! Dar există, de asemenea, un „efect de rotire” M numit Moment (sau Cuplu) care îl echilibrează:
Moment: Forțează ori Distanța în unghi drept.
Știm că Greutatea este 785 N și trebuie, de asemenea, să știm distanța în unghi drept, care în acest caz este de 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Și acel moment este ceea ce oprește fasciculul să se rotească.

Puteți simți momentul când vă țineți de o undiță.
Pe lângă menținerea greutății, trebuie să-l opriți să se rotească în jos.
Fricțiune
Casetă pe o rampă
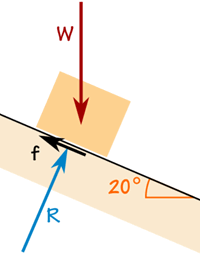
Cutia cântărește 100 kg.
Forța de frecare este suficientă pentru a o menține acolo unde se află.
Forța de reacție R este în unghi drept cu rampă.
Caseta nu accelerează, deci forțele sunt în echilibru:
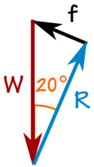
The 100 kg de masă creează o forță descendentă datorită gravitației:
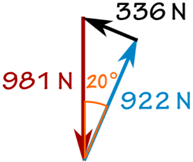
W = 100 kg × 9,81 m / s2 = 981 N
Putem folosi SOHCAHTOA pentru a rezolva triunghiul.
Fricțiune f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reacție N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Și obținem:
Sfaturi pentru a desena diagrame corporale gratuite
- Desenează cât mai simplu posibil. O cutie este adesea suficient de bună.
- Forțele indică direcția în care acționează asupra corpului
- săgețile drepte pentru forțe
- săgețile curbate pentru momente
Sam și Alex Pull a Box
Calculele pot fi uneori mai ușoare atunci când transformăm magnitudinea și direcția în x și y:
 |
< = > |  |
| Vectorul a în coordonate polare | Vectorul a în coordonate carteziene |
Puteți citi cum să le convertiți la Polar și Cartezian Coordonate, dar iată un rezumat rapid:
Să le folosim!