Teste parametrice și non-parametrice pentru compararea a două sau mai multe grupuri

Statistici: teste parametrice și non-parametrice

Această secțiune acoperă:

• Alegerea unui test
• Teste parametrice
• Teste non-parametrice

Alegerea unui test

În ceea ce privește selectarea unui test statistic, cea mai importantă întrebare este „care este ipoteza principală a studiului?” În unele cazuri nu există nicio ipoteză; anchetatorul vrea doar să „vadă ce este acolo”. De exemplu, într-un studiu de prevalență nu există nicio ipoteză de testat, iar dimensiunea studiului este determinată de cât de precis dorește investigatorul să determine prevalența. Dacă nu există nicio ipoteză, atunci nu există nici un test statistic. Este important să se decidă a priori ce ipoteze sunt confirmatoare (adică testează o relație presupusă) și care sunt exploratorii (sunt sugerate de date). Niciun studiu nu poate susține o serie întreagă de ipoteze. Un plan sensibil este de a limita sever numărul ipotezelor de confirmare. Deși este valabil să se utilizeze teste statistice pe ipoteze sugerate de date, valorile P ar trebui utilizate numai ca linii directoare, iar rezultatele tratate ca fiind provizorii până la confirmarea studiilor ulterioare. Un ghid util este utilizarea unei corecții Bonferroni, care afirmă pur și simplu că, dacă se testează n ipoteze independente, ar trebui să se utilizeze un nivel de semnificație de 0,05 / n. Astfel, dacă ar exista două ipoteze independente, un rezultat ar fi declarat semnificativ numai dacă P < 0.025. Rețineți că, deoarece testele sunt rareori independente, aceasta este o procedură foarte conservatoare – adică una care este puțin probabil să respingă ipoteza nulă. Anchetatorul ar trebui apoi să întrebe „datele sunt independente?” Acest lucru poate fi dificil de decis, dar, de regulă, rezultatele pentru același individ sau pentru indivizi similari nu sunt independenți. Astfel, rezultatele dintr-un proces încrucișat sau dintr-un studiu de caz-control, în care controalele au fost potrivite cu cazurile în funcție de vârstă, sex și clasă socială, nu sunt independente. , astfel încât un design asortat ar trebui să fie urmat de o analiză asociată.

Următoarea întrebare este „ce tipuri de date sunt măsurate?” Testul utilizat ar trebui să fie determinat de date. Alegerea testului pentru datele potrivite sau asociate este descrisă în Tabelul 1 și pentru datele independente în Tabelul 2.

Tabelul 1 Alegerea testului statistic din observarea asociată sau asociată

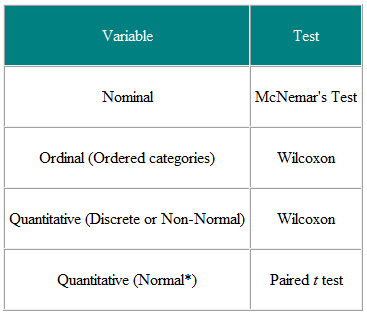
Este util să decideți variabilele de intrare și variabilele de rezultat. De exemplu, într-un studiu clinic, variabila de intrare este tipul de tratament – o variabilă nominală – iar rezultatul poate fi o măsură clinică distribuită în mod normal. Testul necesar este apoi testul t (Tabelul 2). Cu toate acestea, dacă variabila de intrare este continuă, să spunem un scor clinic, iar rezultatul este nominal, să spunem vindecat sau nu vindecat, regresia logistică este analiza necesară. Un test t în acest caz poate ajuta, dar nu ne-ar oferi ceea ce avem nevoie, și anume probabilitatea unei vindecări pentru o anumită valoare a scorului clinic. Ca un alt exemplu, să presupunem că avem un studiu transversal în care întrebăm un eșantion aleatoriu de oameni dacă ei cred că medicul generalist face o treabă bună, pe o scară de cinci puncte, și dorim să ne asigurăm dacă femeile au o opinie mai înaltă a medicilor generaliști decât au bărbații. Variabila de intrare este sexul, care este nominal. Variabila rezultat este scala ordinală în cinci puncte. Opinia fiecărei persoane este independentă de celelalte, deci avem date independente. Din Tabelul 2 ar trebui să folosim un test χ2 pentru tendință sau un test Mann-Whitney U cu o corecție pentru legături (NB o egalitate are loc în cazul în care două sau mai multe valorile sunt aceleași, deci nu există o ordine strict crescătoare a rangurilor – acolo unde se întâmplă acest lucru, se poate face o medie a valorilor pentru valorile legate). Rețineți, totuși, dacă unii oameni împărtășesc un medic generalist, iar alții nu, atunci datele nu sunt Este necesară o analiză independentă și mai sofisticată. Rețineți că aceste tabele ar trebui considerate doar ca ghiduri și că fiecare caz ar trebui luat în considerare pe fondul său.

Tabelul 2 Alegerea testului statistic pentru observații independente

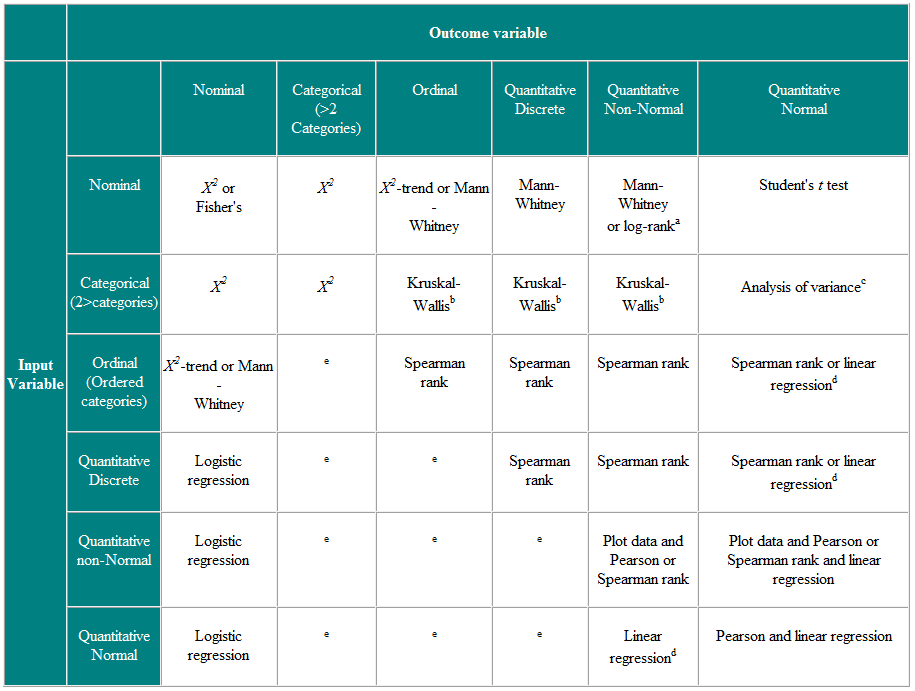
a Dacă datele sunt cenzurate. b Testul Kruskal-Wallis este utilizat pentru compararea variabilelor ordinale sau non-normale pentru mai mult de două grupuri și este o generalizare a testului U Mann-Whitney. c Analiza varianței este o tehnică generală și o versiune (analiza unică a varianței) este utilizată pentru a compara variabilele distribuite în mod normal pentru mai mult de două grupuri și este echivalentul parametric al Kruskal-Wallistest. d Dacă variabila de rezultat este variabila dependentă, atunci cu condiția ca reziduurile (diferențele dintre valorile observate și răspunsurile prezise din regresie) să fie distribuite în mod plauzibil în mod normal, atunci distribuția variabilei independente nu este importantă. e Există o serie de tehnici mai avansate, cum ar fi regresia Poisson, pentru a face față acestor situații. Cu toate acestea, ele necesită anumite ipoteze și este adesea mai ușor să dihotomizați variabila de rezultat sau să o tratați ca fiind continuă. . Aceasta este adesea presupunerea că datele despre populație sunt distribuite în mod normal. Testele non-parametrice sunt „fără distribuție” și, ca atare, pot fi utilizate pentru variabile non-normale. Tabelul 3 prezintă echivalentul non-parametric al unui număr de teste parametrice.

Tabelul 3 Parametric și Testele non-parametrice pentru compararea a două sau mai multe grupuri

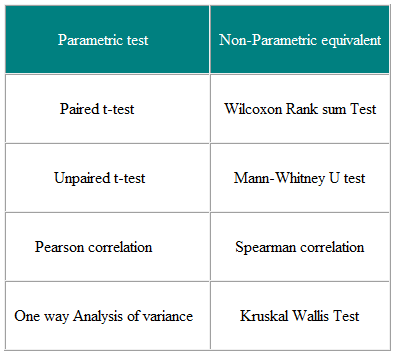
Testele non-parametrice sunt valabile atât pentru datele distribuite în mod normal, cât și pentru Datele distribuite în mod normal, deci de ce să nu le folosim tot timpul?

S-ar părea prudent să folosim teste non-parametrice în toate cazurile, ceea ce ne-ar face să ne deranjăm testarea pentru normalitate. Sunt preferate testele parametrice, totuși, din următoarele motive:

1. Rareori ne interesează doar un test de semnificație; am dori să spunem ceva despre populația din care provin probele și acest lucru este cel mai bine făcut cu
estimări ale parametrilor și intervalelor de încredere.

2. Este dificil să se realizeze modele flexibile cu teste non-parametrice, de exemplu, permițând factorii de confuzie utilizând mai mulți regresie.

3. Testele parametrice au de obicei mai multă putere statistică decât echivalentele lor non-parametrice. Cu alte cuvinte, este mai probabil să detectăm diferențe semnificative atunci când
există cu adevărat.

Testele non-parametrice compară medianele?

Este o credință obișnuită că un Testul Mann-Whitney U este de fapt un test pentru diferențele în mediane. Cu toate acestea, două grupuri ar putea avea aceeași mediană și totuși au un test semnificativ Mann-Whitney U. Luați în considerare următoarele date pentru două grupuri, fiecare cu 100 de observații. Grupa 1: 98 (0), 1, 2; Grupa 2: 51 (0), 1, 48 (2). Mediana în ambele cazuri este 0, dar din testul Mann-Whitney P < 0.0001. Doar dacă suntem pregătiți să facem presupunerea suplimentară că diferența dintre cele două grupuri este pur și simplu o schimbare de locație (adică distribuția datelor într-un grup este pur și simplu mutată cu o sumă fixă de la cealaltă) putem spune că testul este un test al diferenței de mediane. Cu toate acestea, dacă grupurile au aceeași distribuție, atunci o schimbare de locație va muta medianele și mijloacele cu aceeași cantitate și astfel diferența de mediane este aceeași cu diferența de medii. Astfel, testul Mann-Whitney U este, de asemenea, un test pentru diferența de medii. Cum este legat testul Mann-Whitney U de testul t? Dacă cineva ar introduce rândurile datelor, mai degrabă decât datele în sine, într-un program de testare cu două eșantioane, valoarea P obținută ar fi foarte apropiată de cea produsă de un test U al lui Mann-Whitney.