Pentru a determina distribuția unei variabile aleatorii discrete putem furniza fie PMF, fie CDF. Pentru variabilele aleatoare continue, CDF este bine definit, astfel încât să putem furniza CDF. Cu toate acestea, PMF nu funcționează pentru variabilele aleatoare continue, deoarece pentru o variabilă continuă aleatoare $ P (X = x) = 0 $ pentru toți $ x \ in \ mathbb {R} $. În schimb, putem defini funcția densității probabilității (PDF). PDF-ul este mai degrabă densitatea probabilității decât masa probabilității. Conceptul este foarte similar cu densitatea de masă din fizică: unitatea sa este probabilitatea pe unitate de lungime. Pentru a obține un sentiment pentru PDF, luați în considerare o variabilă continuă aleatoare $ X $ și definiți funcția $ f_X (x) $ după cum urmează (oriunde există limita): $$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P (x

$$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X (x + \ Delta) -F_X (x)} {\ Delta} $$ $$ = \ frac {dF_X (x)} {dx} = F ” _X (x), \ hspace {20pt} \ textrm {if} F_X (x) \ textrm {este diferențiat la} x. $$

Astfel, avem următoarea definiție pentru PDF cu variabile aleatoare continue:

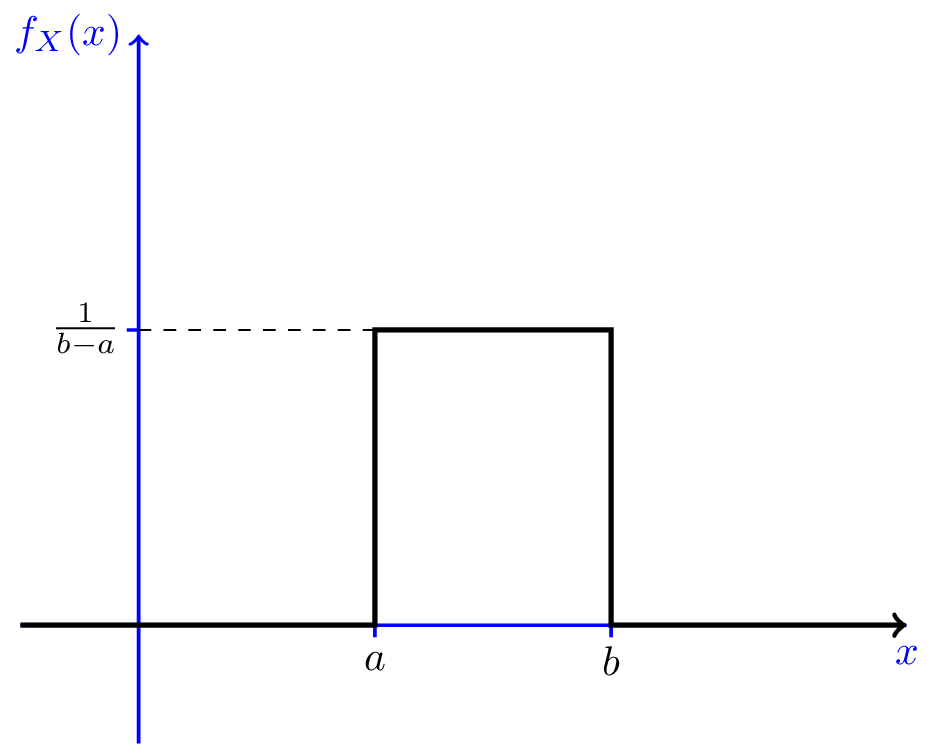
Exemplu
Fie $ X $ o variabilă continuă aleatorie cu următorul PDF \ begin {ecuație} \ nonumber f_X (x) = \ left \ {\ begin {array} {ll} ce ^ {- x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {altfel} \ end {array} \ right. \ end {ecuație} unde este $ c $ o constantă pozitivă.

1. Găsiți $ c $.
2. Găsiți CDF-ul lui X, $ F_X (x) $.
3. Găsiți $ P (1

Gama