Abruptitatea unui deal se numește pantă. Același lucru este valabil și pentru abruptul unei linii. Panta este definită ca raportul dintre schimbarea verticală dintre două puncte, creșterea, și schimbarea orizontală dintre aceleași două puncte, cursa.

$$ panta = \ frac {creștere} {cursă} = \ frac {change \: in \: y} {change \: in \: x} $$

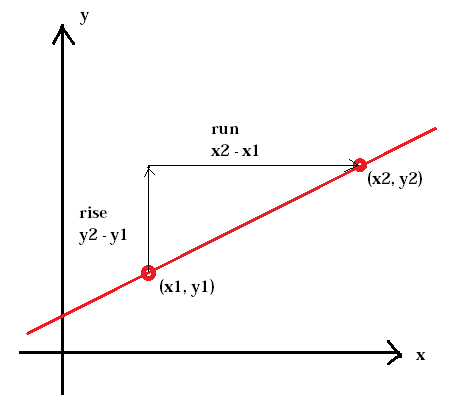
panta unei linii este de obicei reprezentată de litera m. (x1, y1) reprezintă primul punct în timp ce (x2, y2) reprezintă al doilea punct.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Este important să păstrați coordonatele x și y în aceeași ordine atât în numărător, cât și în numitor, altfel veți obține panta greșită.

Exemplu

Găsiți panta liniei

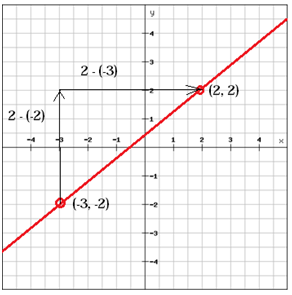
(x1, y1 ) = (-3, -2) și (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ left (-2 \ right)} {2- \ left (-3 \ right)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

O linie cu o pantă pozitivă (m > 0), ca linia de mai sus, crește de la stânga la dreapta în timp ce o linie cu o pantă negativă (m < 0) cade de la stânga la dreapta.

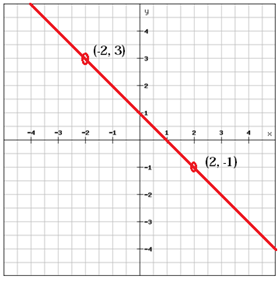
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ left (-1 \ right) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Dacă două linii au aceeași pantă, se spune că liniile sunt p arallel.

Puteți exprima o funcție liniară utilizând forma interceptării pantei.

$$ y = mx + b $$

$$ m = panta $ $

$$ b = y – intercepta $$

Lecție video

Găsește panta