Parametriska och icke-parametriska tester för att jämföra två eller flera grupper

Statistik: Parametriska och icke-parametriska tester

Detta avsnitt täcker:

• Välja ett test
• Parametriska test
• Icke-parametriska test

Välja ett test

När det gäller att välja ett statistiskt test är den viktigaste frågan ”vad är huvudhypotesen för studien?” I vissa fall finns det ingen hypotes; utredaren vill bara ”se vad som finns där”. Till exempel, i en prevalensstudie finns det ingen hypotes att testa, och storleken på studien bestäms av hur exakt utredaren vill bestämma prevalensen. Om det inte finns någon hypotes finns det inget statistiskt test. Det är viktigt att på förhand bestämma vilka hypoteser som är bekräftande (det vill säga testar något förmodat förhållande) och vilka som är utforskande (föreslås av uppgifterna). Ingen enskild studie kan stödja en hel serie hypoteser. En förnuftig plan är att kraftigt begränsa antalet bekräftande hypoteser. Även om det är giltigt att använda statistiska tester på hypoteser som föreslås av data, bör P-värden endast användas som riktlinjer och resultaten behandlas som preliminära tills de bekräftas av efterföljande studier. En användbar guide är att använda en Bonferroni-korrigering, som helt enkelt säger att om man testar n oberoende hypoteser, bör man använda en signifikansnivå på 0,05 / n. Således om det fanns två oberoende hypoteser skulle ett resultat endast förklaras signifikant om P < 0,025. Observera att eftersom test sällan är oberoende är detta ett mycket konservativt förfarande – dvs. en som sannolikt inte kommer att avvisa nollhypotesen. Utredaren bör sedan fråga ”är uppgifterna oberoende?” Detta kan vara svårt att avgöra, men som en tumregel är resultat på samma individ eller från matchade individer inte oberoende. Resultaten från en crossover-studie eller från en fallkontrollstudie där kontrollerna matchades till fallen efter ålder, kön och social klass är inte oberoende.

• Analysen bör återspegla designen , och därför bör en matchad design följas av en matchad analys.
• Resultat mätt över tid kräver särskild försiktighet. Ett av de vanligaste misstagen i statistisk analys är att behandla korrelerade variabler som om de vore oberoende. Antag till exempel att vi tittade på behandling av bensår, där vissa människor hade sår på varje ben. Vi kan ha 20 försökspersoner med 30 sår men antalet oberoende information är 20 eftersom tillståndet för sår på varje ben för en person kan påverkas av tillståndet för personens hälsa och en analys som betraktade sår som oberoende observationer skulle vara felaktiga. För en korrekt analys av blandade och oparade data – kontakta en statistiker.

Nästa fråga är ”vilka typer av data mäts?” Testet som används bör bestämmas av uppgifterna. Valet av test för matchade eller parade data beskrivs i tabell 1 och för oberoende data i tabell 2.

Tabell 1 Val av statistiskt test från parad eller matchad observation

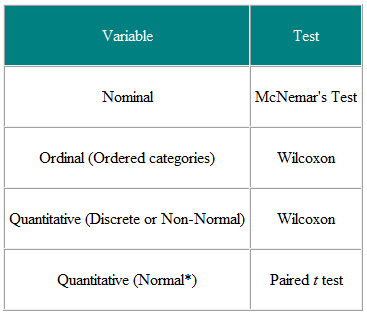
Det är bra att bestämma inmatningsvariablerna och utfallsvariablerna. Till exempel, i en klinisk prövning är ingångsvariabeln typen av behandling – en nominell variabel – och resultatet kan vara någon klinisk åtgärd, kanske normalt fördelad. Det erforderliga testet är sedan t-testet (tabell 2). Men om inmatningsvariabeln är kontinuerlig, säg en klinisk poäng, och resultatet är nominellt, säg botat eller inte botat, är logistisk regression den erforderliga analysen. Ett t-test i detta fall kan hjälpa men skulle inte ge oss vad vi behöver, nämligen sannolikheten för en bot för ett visst värde av den kliniska poängen. Anta att vi har en tvärsnittsstudie där vi frågar ett slumpmässigt urval av människor om de tycker att deras allmänläkare gör ett bra jobb, i fem poäng, och vi vill se om kvinnor har en högre åsikt av allmänläkare än män har. Ingångsvariabeln är kön, vilket är nominellt. Resultatvariabeln är den fempunkts ordinära skalan. Varje persons åsikt är oberoende av de andra, så vi har oberoende data. Från tabell 2 bör vi använda ett χ2-test för trend, eller ett Mann-Whitney U-test med en korrigering för band (OBS en slips förekommer där två eller fler värdena är desamma, så det finns ingen strikt ökande rangordning – där detta händer kan man räkna medelvärdena för bundna värden. Observera dock att om vissa människor delar en allmänläkare och andra inte, så är uppgifterna inte oberoende och det krävs en mer sofistikerad analys. Observera att dessa tabeller endast bör betraktas som riktlinjer och att varje enskilt fall bör övervägas på dess meriter.

Tabell 2 Val av statistiskt test för oberoende observationer

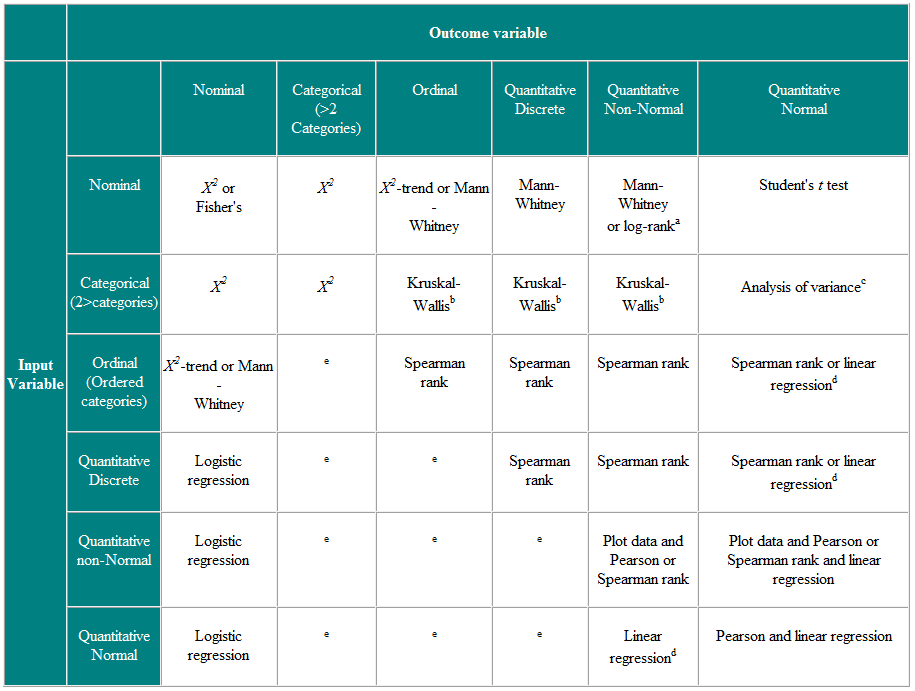
a Om data censureras. b Kruskal-Wallis-testet används för att jämföra ordinala eller icke-normala variabler för mer än två grupper och är en generalisering av Mann-Whitney U-testet. c Variansanalys är en allmän teknik, och en version (envägsanalys av varians) används för att jämföra normalt distribuerade variabler för mer än två grupper och är den parametriska ekvivalenten för Kruskal-Wallistest. d Om utfallsvariabeln är den beroende variabeln, förutsatt att resterna (skillnaderna mellan de observerade värdena och de förutsagda svaren från regression) är troligt Normalt fördelade, så är fördelningen av den oberoende variabeln inte viktig. e Det finns ett antal mer avancerade tekniker, såsom Poisson-regression, för att hantera dessa situationer. De kräver dock vissa antaganden och det är ofta lättare att antingen dikotomisera resultatvariabeln eller behandla den som kontinuerlig.

Parametriska tester är de som gör antaganden om parametrarna för befolkningsfördelningen från vilken urvalet dras. . Detta är ofta antagandet att befolkningsdata normalt distribueras. Icke-parametriska tester är ”distributionsfria” och kan som sådana användas för icke-normala variabler. Tabell 3 visar den icke-parametriska motsvarigheten till ett antal parametriska tester.

Tabell 3 Parametrisk och Icke-parametriska tester för att jämföra två eller flera grupper

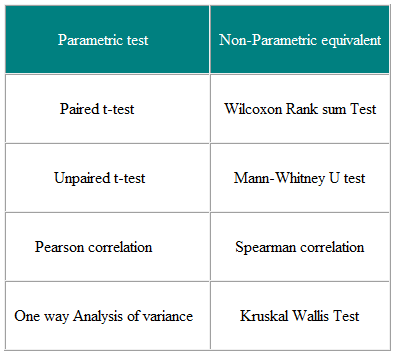
Icke-parametriska tester är giltiga för både icke-normalt distribuerade data och Normalt distribuerad data, så varför inte använda dem hela tiden?

Det verkar klokt att använda icke-parametriska tester i alla fall, vilket skulle spara någon att testa för normalitet. Parametriska tester är att föredra, dock av följande skäl:

1. Vi är sällan intresserade av enbart ett signifikansprov, vi skulle vilja säga något om den population som proverna kom från, och detta görs bäst med
uppskattningar av parametrar och konfidensintervall.

2. Det är svårt att göra flexibel modellering med icke-parametriska tester, till exempel att möjliggöra förvirrande faktorer som använder flera regression.

3. Parametriska tester har vanligtvis mer statistisk kraft än deras icke-parametriska motsvarigheter. Med andra ord är det mer troligt att man upptäcker signifikanta skillnader när de verkligen finns.

Jämför icke-parametriska tester medianer?

Det är en vanligt förekommande tro att en Mann-Whitney U-test är faktiskt ett test för skillnader i medianer. Två grupper kan dock ha samma median och ändå ha ett signifikant Mann-Whitney U-test. Tänk på följande data för två grupper, var och en med 100 observationer. Grupp 1: 98 (0), 1, 2; Grupp 2: 51 (0), 1, 48 (2). Medianen är i båda fallen 0, men från Mann-Whitney-testet P < 0,0001. Endast om vi är beredda att göra det ytterligare antagandet att skillnaden i de två grupperna helt enkelt är en platsförskjutning (det vill säga fördelningen av data i en grupp helt enkelt flyttas med en fast mängd från den andra) kan vi säga att testet är ett test av skillnaden i medianer. Men om grupperna har samma fördelning, flyttar en platsförskjutning medianer och medel med samma mängd och så är skillnaden i medianer densamma som skillnaden i medel. Således är Mann-Whitney U-testet också ett test för skillnaden i medel. Hur är Mann-Whitney U-testet relaterat till t-testet? Om man matar in raden av data snarare än själva data i ett tvåprov-t-testprogram, skulle det erhållna P-värdet vara mycket nära det som produceras av ett Mann-Whitney U-test.