• K-närmaste granne är en av de enklaste maskininlärningsalgoritmerna baserade om övervakad inlärningsteknik.
• K-NN-algoritmen antar likheten mellan det nya fallet / data och tillgängliga fall och placerar det nya fallet i den kategori som mest liknar de tillgängliga kategorierna.
• K-NN-algoritmen lagrar all tillgänglig data och klassificerar en ny datapunkt baserat på likheten. Detta innebär att när nya data dyker upp kan de enkelt klassificeras i en brunnkategori med hjälp av K-NN-algoritmen.
• K-NN-algoritmen kan användas för regression såväl som för klassificering men mestadels används den för klassificeringsproblemen.
• K-NN är en icke-parametrisk algoritm, vilket betyder det antar inget underliggande data.
• Det kallas också en lat eleversalgoritm eftersom den inte lär sig av träningsuppsättningen omedelbart istället lagrar den datasetet och vid klassificeringen utför den en åtgärd på datamängden.
• KNN-algoritmen i träningsfasen lagrar bara datamängden och när den får ny data klassificerar den informationen i en kategori som liknar de nya uppgifterna.
• Exempel: Anta att vi har en bild av en varelse som liknar katt och hund, men vi vill veta om det är en katt eller hund. Så för denna identifiering kan vi använda KNN-algoritmen, eftersom den fungerar på ett likhetsmått. Vår KNN-modell hittar liknande funktioner i den nya datamängden för katter och hundar och baserat på de mest liknande funktionerna kommer den att placeras i antingen katt- eller hundkategori.

Varför behöver vi en K-NN-algoritm?

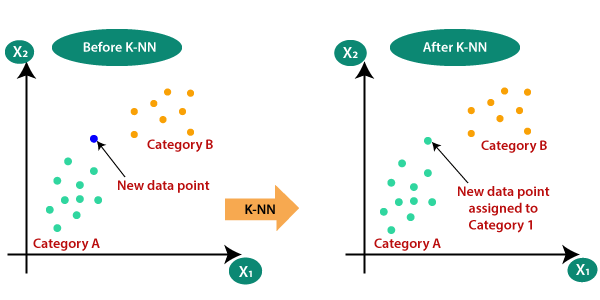
Antag att det finns två kategorier, dvs. kategori A och kategori B, och vi har en ny datapunkt x1, så denna datapunkt ligger i vilken av dessa kategorier. För att lösa denna typ av problem behöver vi en K-NN-algoritm. Med hjälp av K-NN kan vi enkelt identifiera kategorin eller klassen för en viss dataset. Tänk på nedanstående diagram:

Hur fungerar K-NN?

K-NN-arbetet kan förklaras utifrån nedanstående algoritm:

• Steg-1: Välj antalet K för grannarna
• Steg-2: Beräkna det euklidiska avståndet för K-antalet grannar
• Steg 3: Ta K närmaste grannar enligt det beräknade euklidiska avståndet.
• Steg 4: Bland dessa k grannar räknar du antalet datapunkter i varje kategori.
• Steg 5: Tilldela de nya datapunkterna till den kategori som antalet grannar är högst för.
• Steg 6: Vår modell är klar.

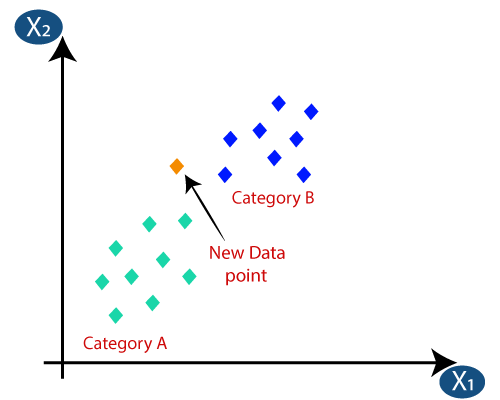
Antag att vi har en ny datapunkt och vi måste placera den i önskad kategori. Tänk på bilden nedan:

• För det första väljer vi antalet grannar, så vi väljer k = 5.
• Därefter beräknar vi det euklidiska avståndet mellan datapunkterna. Det euklidiska avståndet är avståndet mellan två punkter, som vi redan har studerat i geometri. Det kan beräknas som:

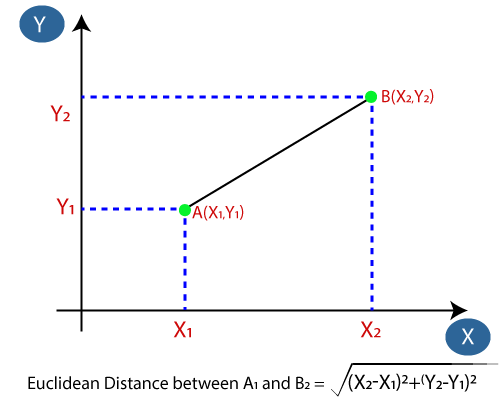
• Genom att beräkna det euklidiska avståndet fick vi närmaste grannar, som tre närmaste grannar i kategori A och två närmaste grannar i kategori B. Tänk på bilden nedan:

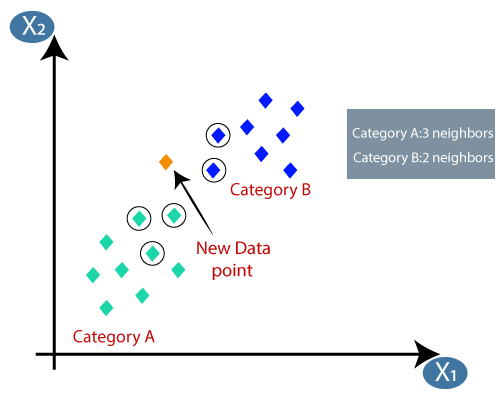
• Som vi kan se är de 3 närmaste grannarna från kategori A, därför måste denna nya datapunkt tillhöra kategori A.

Hur väljer man värdet för K i K-NN-algoritmen?

Nedan följer några punkter till kom ihåg när du valde värdet på K i K-NN-algoritmen:

• Det finns inget särskilt sätt att bestämma det bästa värdet för ”K”, så vi måste prova några värden för att hitta det bästa av dem. Det mest föredragna värdet för K är 5.
• Ett mycket lågt värde för K såsom K = 1 eller K = 2, kan vara bullrigt och leda till effekterna av outliers i modellen.
• Stora värden för K är bra, men det kan hitta vissa svårigheter.

Fördelar med KNN-algoritm:

• Det är enkelt att implementera.
• Det är robust mot de bullriga träningsuppgifterna
• Det kan vara mer effektivt om träningsdata är stora.

Nackdelar med KNN-algoritm:

• Behöver alltid bestämma värdet på K som kan vara komplicerat någon gång.
• Beräkningskostnaden är hög på grund av att man beräknar avståndet mellan datapunkterna för alla träningsprover .

Pythonimplementering av KNN-algoritmen

För att göra Python-implementeringen av K-NN-algoritmen kommer vi att använda samma problem och dataset som vi har använt i Logistisk återgång. Men här kommer vi att förbättra modellens prestanda. Nedan följer problembeskrivningen:

Problem för K-NN-algoritm: Det finns ett biltillverkningsföretag som har tillverkat en ny SUV-bil.Företaget vill ge annonserna till de användare som är intresserade av att köpa SUV: n. Så för detta problem har vi en datauppsättning som innehåller information om flera användare via det sociala nätverket. Datauppsättningen innehåller mycket information men den beräknade lönen och åldern kommer vi att beakta för den oberoende variabeln och den köpta variabeln är för den beroende variabeln. Nedan finns datauppsättningen:

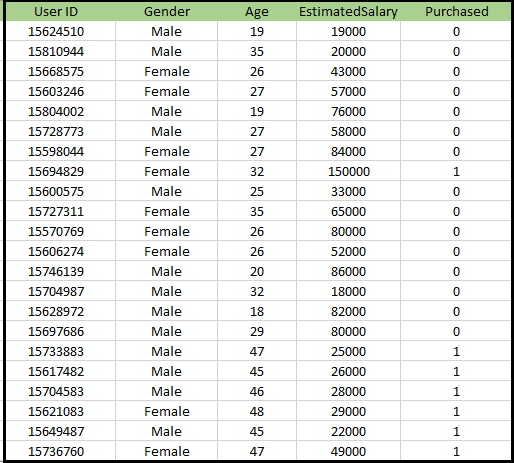
Steg för att implementera K-NN-algoritmen:

• Databehandlingssteg
• Anpassa K-NN-algoritmen till träningsuppsättningen
• Förutsäga testresultatet
• Testens noggrannhet (skapande av förvirringsmatris)
• Visualisera testuppsättningsresultatet.

Steg för databearbetning:

Steget för databehandlingen förblir exakt detsamma som logistisk regression. Nedan följer koden för det:

Genom att köra ovanstående kod importeras vår dataset till vårt program och förbehandlas väl. Efter funktionsskalning kommer vår testdataset att se ut:

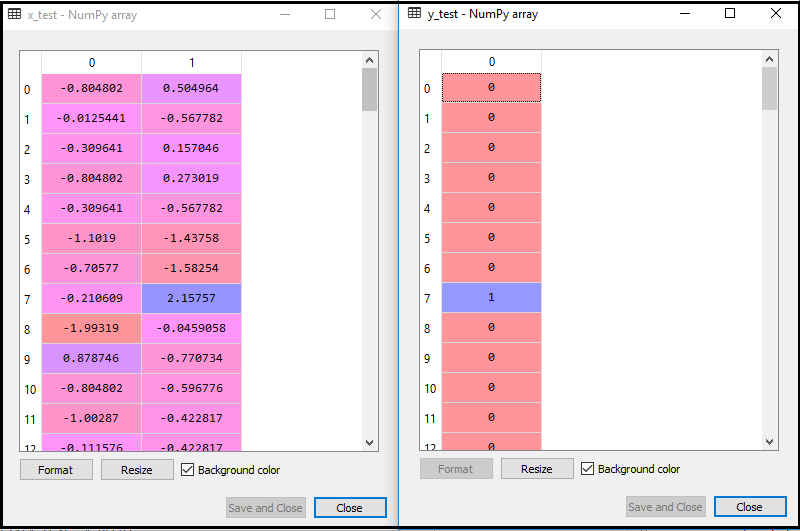
Från ovanstående utdata im ålder kan vi se att våra data har framgångsrikt skalats.

• Anpassa K-NN-klassificeraren till träningsdata:
  Nu passar vi K-NN-klassificeraren till träningsdata. För att göra detta importerar vi KNeighborsClassifier-klassen i Sklearn Neighbors-biblioteket. Efter att ha importerat klassen skapar vi klassificeringsobjektet för klassen. Parametern för denna klass kommer att vara
  • n_nära hamnar: Att definiera algoritmens erforderliga grannar. Vanligtvis tar det 5.
  • metric = ”minkowski”: Detta är standardparametern och det bestämmer avståndet mellan punkterna.
  • p = 2: Det motsvarar standarden Euklidiskt mått.

  Och sedan passar vi klassificeraren till träningsdata. Nedan är koden för den:

Output: Genom att köra ovanstående kod får vi utdata som:

• Förutsäga testresultatet: För att förutsäga testuppsättningsresultatet skapar vi en y_pred-vektor som vi gjorde i Logistic Regression. Nedan är koden för den:

Output:

Utgången för ovanstående kod kommer att vara:

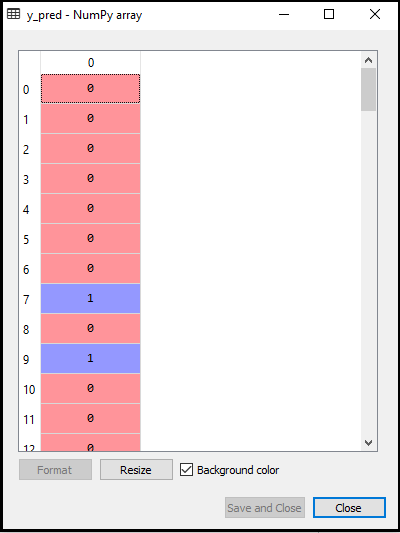
• Skapa förvirringsmatris:
  Nu skapar vi förvirringsmatris för vår K-NN-modell för att se klassificeringens noggrannhet. Nedan är koden för den:

I ovanstående kod har vi importerat confusion_matrix-funktionen och kallat den med variabeln cm.

Output: Genom att köra ovanstående kod får vi matrisen enligt nedan:

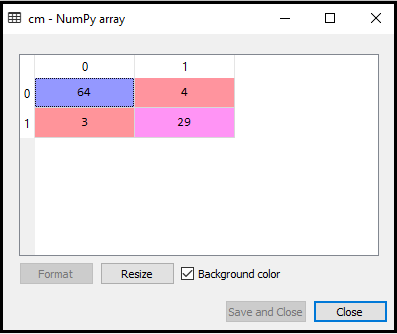
I ovanstående bild kan vi se det finns 64 + 29 = 93 korrekta förutsägelser och 3 + 4 = 7 felaktiga förutsägelser, medan det i logistisk regression fanns 11 felaktiga förutsägelser. Så vi kan säga att modellens prestanda förbättras med hjälp av K-NN-algoritmen.

• Visualisering av träningsuppsättningsresultatet:
  Nu kommer vi att visualisera utbildningsuppsättningsresultatet för K -NN-modell. Koden kommer att förbli densamma som vi gjorde i Logistic Regression, förutom grafens namn. Nedan är koden för det:

Output:

Genom att köra ovanstående kod får vi nedanstående diagram:

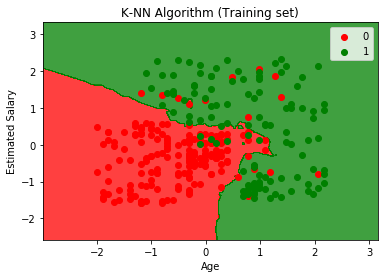
Utgångsdiagrammet skiljer sig från grafen som vi har inträffat i logistisk regression. Det kan förstås i punkterna nedan:

• Som vi kan se visar grafen den röda punkten och de gröna punkterna. De gröna punkterna är för köpta (1) och röda punkter för ej köpta (0) variabel.
• Grafen visar en oregelbunden gräns istället för att visa någon rak linje eller någon kurva eftersom det är en K-NN-algoritm, dvs att hitta närmaste granne.
• Grafen har klassificerat användare i de rätta kategorierna eftersom de flesta användare som inte köpte SUV: n är i den röda regionen och användare som köpte SUV: n är i det gröna området.
• Grafen visar bra resultat men ändå finns det några gröna punkter i den röda regionen och röda punkter i den gröna regionen. Men det här är ingen stor fråga, eftersom man genom att göra den här modellen förhindras att överanpassa problem.
• Därför är vår modell välutbildad.
• Visualisering av testuppsättningsresultatet:
  Efter utbildningen av modellen kommer vi nu att testa resultatet genom att sätta en ny dataset, dvs. Testdataset. Koden förblir densamma utom några mindre ändringar: som x_train och y_train kommer att ersättas med x_test och y_test.
  Nedan följer koden för det:

Output:

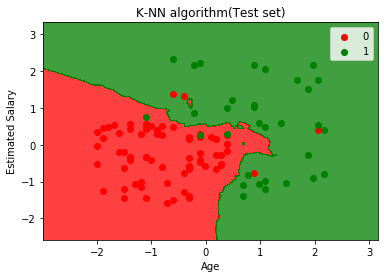
Diagrammet ovan visar utdata för testdatauppsättningen. Som vi kan se i diagrammet är den förutspådda utsignalen väl bra eftersom de flesta av de röda punkterna är i den röda regionen och de flesta av de gröna punkterna finns i det gröna området.

Det finns dock få gröna punkter i det röda området och några röda punkter i det gröna området. Så det här är de felaktiga observationerna som vi har observerat i förvirringsmatrisen (7 Felaktig utmatning).