Kraftberäkningar

Kraft är push eller pull.
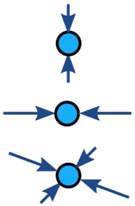
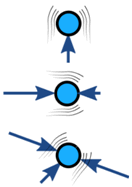
Krafterna på ett objekt är vanligtvis balanserade (om det är obalanserat accelererar objektet):
 |
 |
|
| Balanserad | Obalanserad | |
|---|---|---|
| Ingen acceleration | Acceleration |
Exempel: Krafterna på toppen av detta bryggtorn är i balans (det accelererar inte):

Kablarna drar nedåt lika åt vänster och höger, och det balanseras av tornets tryck uppåt (skjuter tornet? Ja! Tänk dig att du står där istället för tornet.)
Vi kan modellera krafterna så här:

Och när vi sätt dem huvud mot svans ser vi att de stänger tillbaka sig själva, vilket betyder att nettoeffekten är noll:

Krafterna är i balans.
Krafter i balans sägs vara i jämvikt: det finns ingen förändring i rörelse.
Diagram över fria kroppar
Det första steget är att rita ett frikroppsdiagram (även kallat ett kraftdiagram)
Gratis kroppsdiagram: En skiss där en kropp skärs fri från världen utom de krafter som verkar på den.
I bryggsexemplet är det fria kroppsdiagrammet för toppen av tornet:

Free Body Diagram
Det hjälper oss att tänka tydligt om de krafter som verkar på kroppen.
Exempel: Bil på en motorväg
Vilka är krafterna på en bil som kör längs motorvägen?

Motorn arbetar hårt, så varför fortsätter inte bilen att accelerera?
Eftersom körningen kraft balanseras av:
- Luftmotstånd (uttryckt: th luftmotstånd trycks runt),
- Rullmotstånd, även kallat rullfriktion (däcken motstår att deras form ändras)

Free Body Diagram
W är bilens vikt,
R1 och R2 är däckens rullmotstånd,
N1 och N2 är reaktionskrafterna (balanserar bilens vikt).
Obs: stålhjul (som på tåg) har mindre rullmotstånd, men är alldeles hala på vägen!
Beräkningar
Kraft är en vektor. En vektor har storlek (storlek) och riktning:

Vi kan modellera krafterna genom att rita pilar med rätt storlek och riktning . Så här:
Exempel: Beundra utsikten
Brady står på kanten av en balkong som stöds av en horisontell balk och en stag:

Han väger 80 kg.
Vilka är krafterna?
Låt oss ta den plats han står på och tänka på krafterna just där:

Hans vikt
Hans 80 kg massa skapar en nedåtriktad kraft på grund av tyngdkraften.
Kraft är massa gånger acceleration: F = ma
Acceleration på grund av gravitation på jorden är 9,81 m / s2 , så a = 9,81 m / s2
F = 80 kg × 9,81 m / s2
F = 785 N
De andra krafterna
Krafterna är balanserade, så de bör stänga av sig själva så här:

Vi kan använda trigonometri för att lösa det .
Eftersom det är en rätvinklig triangel, kommer SOHCAHTOA att hjälpa.
För Beam, vi känner den angränsande, vi vill veta motsatsen, och ”TOA” säger att vi ska använda Tangent:
solbränna (60 ° ) = Beam / 785 N
Beam / 785 N = tan (60 °)
Beam = tan (60 °) × 785 N
Beam = 1.732 … × 785 N = 1360 N
För strut, vi känner den angränsande, vi vill veta hypotenusen, och ”CAH” säger oss att använda Cosine:
cos (60 °) = 785 N / Strut
Strut × cos (60 °) = 785 N
Strut = 785 N / cos (60 °)
Strut = 785 N / 0.5 = 1570 N
Löst:

Intressant hur mycket kraft som finns på balk och stag jämfört med vikten som stöds!
Moment (eller Moment)
Vad händer om balken bara fastnar i väggen (kallas en cantilever)?

Det finns inget stödjande stöd, så vad händer med krafterna?
Diagrammet för fri kropp ser ut så här:

Den uppåtgående kraften R balanserar den nedåtgående vikten.
Med bara de två tvingar strålen att snurra som en propeller! Men det finns också en ”vändningseffekt” M som kallas Moment (eller vridmoment) som balanserar den:
Moment: Force gånger avståndet i rät vinkel.
Vi vet att vikten är 785 N, och vi måste också veta avståndet i rät vinkel, vilket i detta fall är 3,2 m.
M = 785 N x 3,2 m = 2512 Nm
Och det ögonblicket är det som hindrar strålen från att rotera.

Du kan känna ett ögonblick när du håller i en fiskespö.
Förutom att hålla upp vikten måste du hindra den från att rotera nedåt.
Friktion
Ruta på en ramp
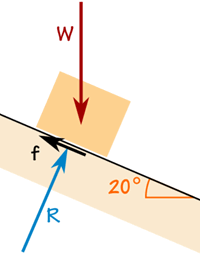
Lådan väger 100 kg.
Friktionskraften är tillräcklig för att hålla den där den är.
Reaktionskraften R är i rät vinkel mot ramp.
Lådan accelererar inte, så krafterna är i balans:
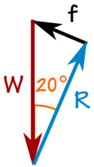
De 100 kg massa skapar en nedåtgående kraft på grund av tyngdkraften:
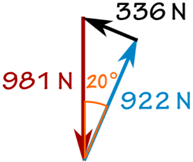
W = 100 kg × 9,81 m / s2 = 981 N
Vi kan använda SOHCAHTOA för att lösa triangeln.
Friktion f:
sin (20 °) = f / 981 N
f = sin (20 °) × 981 N = 336 N
Reaktion N:
cos (20 °) = R / 981 N
R = cos (20 °) × 981 N = 922 N
Och vi får:
Tips för att rita fria kroppsdiagram
- Rita så enkelt som möjligt. En låda är ofta tillräckligt bra.
- Krafter pekar i den riktning de verkar på kroppen
- raka pilar för krafter
- böjda pilar för ögonblick
Sam och Alex Pull a Box
Beräkningarna kan ibland vara enklare när vi förvandlar storlek och riktning till x och y:
 |
< = > |  |
| Vector a i Polar koordinater |
Vector a i kartesisk koordinater |
Du kan läsa om hur du konverterar dem på Polar och Cartesian Koordinater, men här är en snabb sammanfattning:
Låt oss använda dem!