Brantheten för en kulle kallas en sluttning. Detsamma gäller för brantheten i en linje. Lutningen definieras som förhållandet mellan den vertikala förändringen mellan två punkter, stigningen, till den horisontella förändringen mellan samma två punkter, körningen.

$$ lutning = \ frac {rise} {run} = \ frac {ändra \: i \: y} {ändra \: i \: x} $$

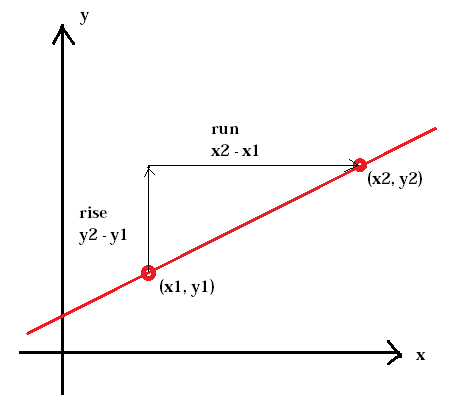
lutning av en linje representeras vanligtvis av bokstaven m. (x1, y1) representerar den första punkten medan (x2, y2) representerar den andra punkten.

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2 } \, -x_ {1}} $$

Det är viktigt att hålla x- och y-koordinaterna i samma ordning i både täljaren och nämnaren annars får du fel lutning.

Exempel

Hitta linjens lutning

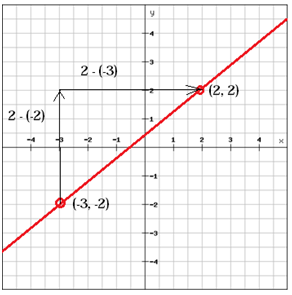
(x1, y1 ) = (-3, -2) och (x2, y2) = (2, 2)

$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ { 2} \, -x_ {1}} = \ frac {2- \ vänster (-2 \ höger)} {2- \ vänster (-3 \ höger)} = \ frac {2 + 2} {2 + 3} = \ frac {4} {5} $$

En linje med en positiv lutning (m > 0), som linjen ovan, stiger från vänster till höger medan en linje med negativ lutning (m < 0) faller från vänster till höger.

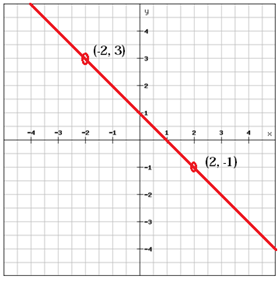
$$ m = \ frac {y_ {2} \, -y_ {1}} {x_ {2} \, -x_ {1}} = \ frac {\ vänster (-1 \ höger) -3} {2- \ left (-2 \ right)} = \ frac {-1-3} {2 + 2} = \ frac {-4} {4} = – 1 $$

Om två linjer har samma lutning sägs linjerna vara p arallel.

Du kan uttrycka en linjär funktion med lutningsavlyssningsformuläret.

$$ y = mx + b $$

$$ m = lutning $ $

$$ b = y – avlyssning $$

Videolektion

Hitta lutningen