MATH 1314: College Algebra (Svenska)
Även om vertikala asymptoter beskriver beteendet hos en graf eftersom utdata blir mycket stora eller mycket små, hjälper horisontella asymptoter att beskriva beteendet hos en graf som ingången blir mycket stor eller mycket liten. Kom ihåg att en polynoms slutbeteende kommer att spegla den ledande termen. Likaså kommer en rationell funktions slutbeteende att spegla förhållandet mellan de ledande termerna för täljaren och nämnarens funktioner.
Det finns tre distinkta resultat när man letar efter horisontella asymptoter:
Fall 1: Om nämnarens grad > -graden för täljaren finns en horisontell asymptot vid y = 0.

Fall 2: Om graden av nämnaren < graden av täljaren med en får vi en sned asymptot.

Lägg märke till att medan grafen för en rationell funktion aldrig kommer att korsa en vertikal asymptot, kan grafen kanske inte korsa en horisontell eller sned som ymptote. Även om grafen för en rationell funktion kan ha många vertikala asymptoter, kommer diagrammet att ha högst en horisontell (eller sned) asymptot.
Det bör noteras att om graden av täljaren är större än graden av nämnaren med mer än en, kommer grafens slutbeteende att efterlikna beteendet hos den reducerade ändbeteendefraktionen. Till exempel om vi hade funktionen
med slutbeteende
grafens slutbeteende skulle se ut som en jämn polynom med en positiv ledande koefficient.
En allmän anmärkning: Horisontella asymptoter för rationella funktioner
Den horisontella asymptoten för en rationell funktion kan vara bestäms genom att titta på täljarens och nämnarens grader.
- Täljarens grad är mindre än nämnarens grad: horisontell asymptot vid y = 0.
- Täljarens grad är större än graden av nämnare med en: ingen horisontell asymptot; sned asymptot.
- Täljarens grad är lika med nämnarens grad: horisontell asymptot i förhållandet mellan ledande koefficienter.
Exempel 9: Identifiera horisontella och vertikala asymptoter
Hitta de horisontella och vertikala asymptoterna för funktionen
Lösning
Observera först att den här funktionen inte har några gemensamma faktorer, så det finns inga potentiella borttagbara diskontinuiteter.
Funktionen har vertikala asymptoter när nämnaren är noll, vilket gör att funktionen är odefinierad. Nämnaren är noll vid x = 1, -2, text {och} 5 \, vilket indikerar vertikala asymptoter vid dessa värden.
Täljaren har grad 2, medan nämnaren har grad 3. Eftersom graden av nämnaren är större än graden av täljaren, kommer nämnaren att växa snabbare än täljaren, vilket får utgångarna att tendera mot noll när ingångarna blir stora, och så som xto pm infty, fleft (xright) till 0 \. Den här funktionen har en horisontell asymptot vid y = 0 \.
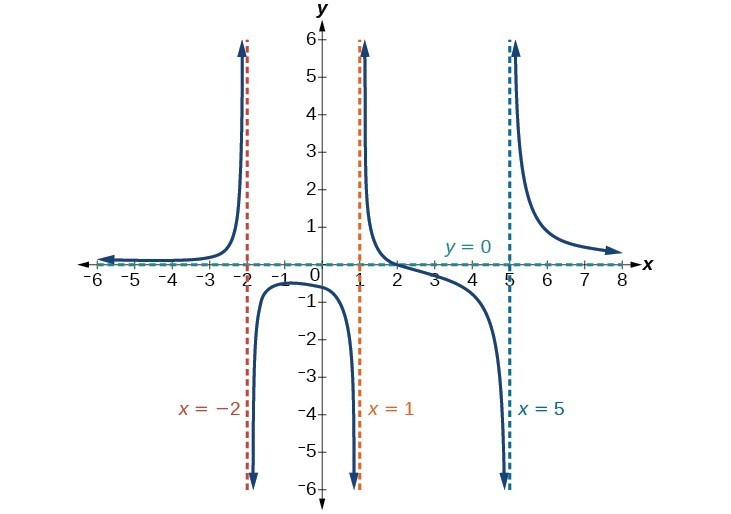
Figur 15
En allmän anmärkning: Avlyssningar av rationella funktioner
En rationell funktion har en y-skärning när ingången är noll, om funktionen är definierad som noll. En rationell funktion kommer inte att ha en y-skärning om funktionen inte är definierad vid noll.
På samma sätt kommer en rationell funktion att ha x-avlyssningar vid ingångarna som orsakar att utgången är noll. Eftersom en bråk bara är lika med noll när täljaren är noll, kan x-avlyssningar endast uppstå när täljaren för den rationella funktionen är lika med noll.
Prova det 7
Med tanke på den ömsesidiga kvadratfunktionen som flyttas åt höger 3 enheter och ner 4 enheter, skriv detta som en rationell funktion. Hitta sedan x– och y-avlyssningar och de horisontella och vertikala asymptoterna.
Lösning