För att bestämma fördelningen av en diskret slumpmässig variabel kan vi antingen tillhandahålla dess PMF eller CDF. För kontinuerliga slumpmässiga variabler är CDF väldefinierad så att vi kan tillhandahålla CDF. PMF fungerar dock inte för kontinuerliga slumpmässiga variabler, för för en kontinuerlig slumpmässig variabel $ P (X = x) = 0 $ för alla $ x \ i \ mathbb {R} $. Istället kan vi vanligtvis definiera sannolikhetsdensitetsfunktionen (PDF). PDF-filen är densitetens sannolikhet snarare än sannolikhetsmassan. Konceptet liknar väldigt massmassa i fysik: dess enhet är sannolikhet per längdenhet. För att få en känsla för PDF, överväg en kontinuerlig slumpmässig variabel $ X $ och definiera funktionen $ f_X (x) $ enligt följande (varhelst gränsen finns): $$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0 ^ +} \ frac {P (x

$$ f_X (x) = \ lim _ {\ Delta \ rightarrow 0} \ frac {F_X (x + \ Delta) -F_X (x)} {\ Delta} $$ $$ = \ frac {dF_X (x)} {dx} = F ” _X (x), \ hspace {20pt} \ textrm {if} F_X (x) \ textrm {är differentierbar vid} x. $$

Således har vi följande definition för PDF av kontinuerliga slumpmässiga variabler:

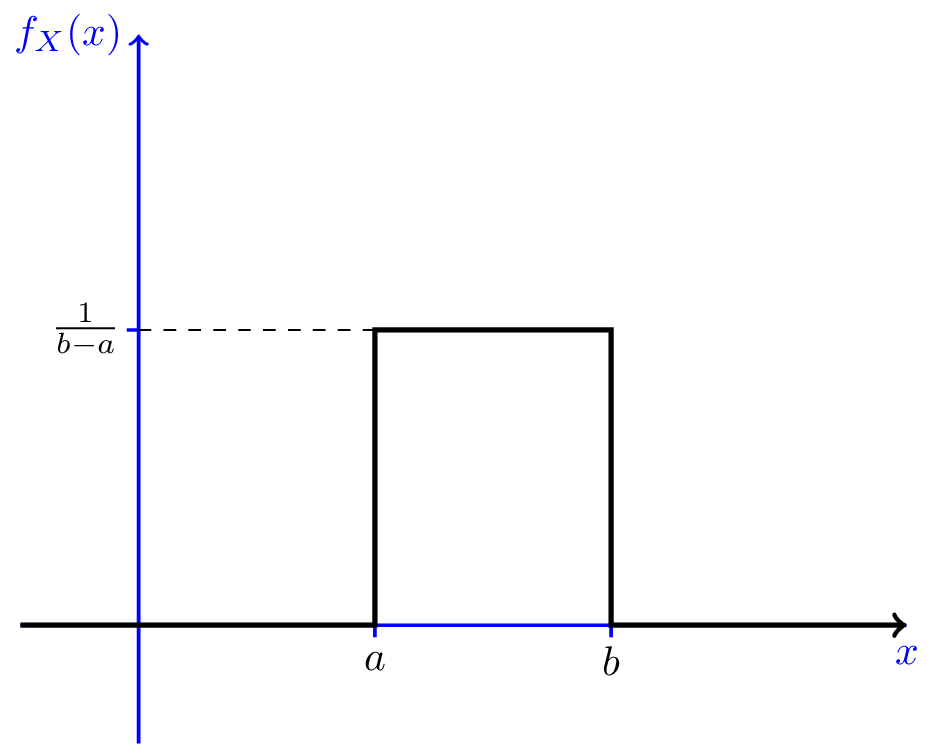
Exempel
Låt $ X $ vara en kontinuerlig slumpmässig variabel med följande PDF \ begin {ekvation} \ nonumber f_X (x) = \ left \ {\ begin {array} {ll} ce ^ {- x} & \ quad x \ geq 0 \\ 0 & \ quad \ text {annars} \ end {array} \ höger. \ end {ekvation} där $ c $ är en positiv konstant.

1. Hitta $ c $.
2. Hitta CDF för X, $ F_X (x) $.
3. Hitta $ P (1

Räckvidd